reverse overshot water wheel quotation

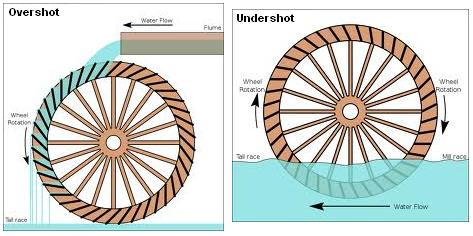
Frequently used in mines and probably elsewhere (such as agricultural drainage), the reverse overshot water wheel was a Roman innovation to help remove water from the lowest levels of underground workings. It is described by Vitruvius in his work

The Roman author Vitruvius gives explicit instructions on the construction of dewatering devices, and describes three variants of the "tympanum" in Chapter X of

Pliny the Elder is probably referring to such devices in a discussion of silver/lead mines in his silver in his time, many of the silver mines having been started by Hannibal. One of the largest had galleries running for between one and two miles into the mountain, "water-men" (in Latin "aquatini") draining the mine, and they

That they stood suggests that they operated the wheels by standing on the top to turn the cleats, and continuous working would produce a steady stream of water.

Fragments of such machines have been found in mines which were re-opened in the Victorian era in Spain, especially at Rio Tinto, where one example used no less than 16 such wheels working in pairs, each pair of wheels lifting water about 3.5 metres (11 ft), so giving a total lift of 30 metres (98 ft). The system was carefully engineered, and was worked by individuals treading slats at the side of each wheel. It is not an isolated example, because Oliver Davies mentions examples from the Tharsis copper mine and Logroño in Spain, as well as from Dacia. The gold deposits in Dacia, now modern Romania were especially rich, and worked intensively after the successful Roman invasion under Trajan. According to Oliver Davies, one such sequence discovered at Ruda in Hunedoara County in modern Romania was 75 metres (246 ft) deep. If worked like the Rio Tinto example, it would have needed at least 32 wheels.

One such wheel from Spain was rescued and part of it is now on display in the British Museum. Some of the components are numbered, suggesting that it was prefabricated above ground before assembly in the underground passages. In the 1930s, a fragment of a wooden bucket from a drainage wheel was found in deep workings at the Dolaucothi gold mine in west Wales, and is now preserved in the National Museum of Wales in Cardiff. It has been carbon dated to about 90 AD. From the depth of 50 metres (160 ft) below known open workings, it can be inferred that the drainage wheel was part of a sequence just like that found in Spain. The shape of the edge of one of the lifting buckets is almost identical with that from Spain, suggesting that a template was used to make the devices.

They were also used in series, so increasing the lift of water from the workings. However, they must have been more difficult to operate since the user had to stand on a slanting surface to turn the screw. The steeper the incline, the greater the risk of the user slipping from the top of the screw. No doubt the reverse water wheel was easier to use with a horizontal treading surface. On the other hand, the screw could be operated by a crank handle fitted to the central axle, but would be more tiring since the weight of the operator does not bear on the crank, as it does when trod from above.

Like the reverse water wheel, the cochlea was used for many other purposes apart from draining mines. Irrigation of farmland would have been the most popular application, but any activity which involved lifting water would have employed the devices.

Multiple sequences of water wheels were used elsewhere in the Roman Empire, such as the famous example at Barbegal in southern France. This system was also a stack of 16 wheels but worked like a normal overshot wheel, the wheels driving stone mills and used to grind grains. The water mills were worked from a masonry aqueduct supplying the Roman town at Arles, and the remains of the masonry mills are still visible on the ground today, unlike the underground drainage systems of the mines, which were destroyed by later mining operations. Other such sequences of mills existed on the Janiculum in Rome, but have been covered and changed by later buildings built on top of them.

To explain the mechanism for this surface ferroportin-independent Fe exit, we explored the possibility of GAPDH-mediated apotransferrin trafficking into cells for sequestration and evacuation of intracellular Fe. This could involve a process akin to receptor-mediated trafficking of holotransferrin into cells for intracellular Fe delivery, followed by recycling of the residual apotransferrin along with receptor back to the cell surface, but instead operating in reverse. Such a form of retroendocytosis has previously been described for high-density lipoprotein (HDL) and apolipoprotein A-I endocytosis (followed by recycling and secretion) in diverse cell types (including macrophages), and has been linked to lipid intake and cholesterol efflux (Azuma et al., 2009; Pagler et al., 2006; Röhrl and Stangl, 2013). Fe-loaded J774, THP1 and CHO-TRVb cells all demonstrated a significant increase in internalization of radiolabeled apotransferrin, whereas GAPDH-knockdown THP1 and CHO-TRVb cells failed to increase apotransferrin uptake (Fig. 2A). Confocal microscopy analysis demonstrated the colocalization of GAPDH (that was initially resident on the cell surface) with apotransferrin within Fe-loaded cells (Fig. 2B; Fig. S2A). Immunoelectron microscopy analysis also revealed the presence of both proteins in endosomes of CHO-TRVb cells (Fig. 2Di,Dii). Co-immunoprecipitation of biotinylated apotransferrin with GAPDH from Fe-loaded CHO-TRVb and J774 cell endosomes (Fig. 2E), and an acceptor-photobleaching-based Förster resonance energy transfer (FRET) assay (Fig. 2F) confirmed the interaction between the two internalized proteins. The FRET efficiency measured was 27.79%±6.2 (mean±s.d.) (Fig. 2G).

In summary, our current findings suggest that GAPDH mediates the internalization of apotransferrin to facilitate Fe export through treadmilling of this Fe carrier in and out of cells in a manner reminiscent of the reverse overshot water-wheel, which has been in use since antiquity to pump out water from flooded mines. To date, the movement of transition metal ions out of cells has been considered to be only through transmembrane ion channels, and our current results reveal a totally new dimension to cellular metal ion export and also highlight the higher-order multifunctional nature of GAPDH in the maintenance of cellular Fe homeostasis. A schematic representation of this process is presented in Fig. 6.

A section of a large Roman water-wheel used in draining the enormous copper mines along the Rio Tinto in Andalucía. Intricate networks of reverse-overshot wheels were used in the mines with one section using 16 pairs of wheels to raise water 100 ft. 1st-2nd century AD

The use of multiple sequences of water wheels was used elsewhere in the Roman Empire, such as the famous example at Barbegal in southern France. This system was also a stack of 16 wheels but worked like a normal overshot wheel, the wheels driving stone mills and used to grind corn. The water mills were worked from a masonry aqueduct supplying the Roman town at Arles, and the remains of the masonry mills are still visible on the ground today, unlike the underground drainage systems of the mines, which were destroyed by later mining operations. Other such sequences of mills existed on the Janiculum in Rome, but have been covered and changed by later buildings built on top of them.

The true principle of the tangential wheel was illustrated and described by Branca in 1629. This device was used in Loretto, Italy, and is pictured as a horizontal wheel with vanes or buckets, upon which a jet of steam impinged, causing rotation. This was imparted through a bevel-gear to a shaft that dropped pestles into respective mortars for grinding, as in a stamp-mill. In later times Poncelet (1827) demonstrated the inefficiency of flat vanes, and substituted therefor forms which were concave and tangent to the jet, so that the water, on entering, would run up inclines and back again, thus imparting energy to the water-wheel during its entire course. This was the first form of tangential wheel to “ provide graduated entrances and avoid shocks, concussions or eddies in the water.” Prior to 1822, however, James White had used semi-circular buckets; and in 1843 Madame de Girard of Paris brought out the semi-circular buckets which have since become widely known as the distinctive feature of the Girard water-wheel. De Canson (1847) used quarter-circle buckets to which the jet was applied normally, the water escaping tangentially. Borda, in his memoirs (1767), gave the sum and substance of tangential water-wheel principles when he wrote : “ To produce its total mechanical effects, the water serving as a motive power must be brought on to the wheel with impulse, and quit it without velocity.” Euler’s description of the first-constructed turbine (1754) considered the motion of water in a semi-circle, while imparting power to a wheel. Dingler (1858) gave forms of water-ways which conform well with the half-circle motion of water in driving a tangential wheel. Navier (1819) refers to the mills of Provence and portions of Dauphiny, which had spoon-shaped buckets, receiving the stroke of water, delivered generally through inclined troughs. Again, in 1819, Navier wrote : “ The necessity of disposing machines in such wise that there should be no shock, although established long ago, both by theory and practice, is not so generally recognized as could be desired.

Mr. Brewster also announces that he has frequently had the idea that a hydraulic machine of great efficiency could be constructed by combining the impulsion with the reaction of water.” Ferguson (1826) described an undershot wheel, having buckets inclined to the radius and “ driven partly by impulse.” Schwamkrug, prior to 1850, constructed vertical tangential wheels with outward flow. In short, numerous other instances might be cited to prove that the modern tangential water-wheel has been brought to its present state of high efficiency through gradual evolution from times of antiquity.

In bold relief, however, stand the names of a few men who, in recent years, have developed these wheels from the crude devices of the first part of the century to the high plane which they now occupy as prime movers in the industry of the world. To make reference to the work of these inventors, and then to discuss the engineering features involved in the design and construction of highly efficient tangential -water-wheels, and to consider the tendency of modern practice in this respect, is the purpose of this paper.

Tangential water-wheels are essentially a Californian development, in that their perfection was brought about through the natural conditions imposed in the mining regions of the Golden State, where limited quantities of water at high heads constituted practically the only form of water-power available for the working of mines and mills. But the use of water in limited quantities at high heads necessitated the use of a form of water-wheel entirely distinct from the familiar undershot and overshot types. Others, however, had been working on the same problem as that which confronted the California pioneers, and among these was notably Jearum Atkins, to whom must undoubtedly be given the credit for having been the first to grasp the true principles underlying the operation of the tangential water-wheel by impulse and reaction, and to design a wheel of this type which soundly embodied modern ideas in that direction. The remarkably advanced mechanical ideas of Atkins were first brought before the engineering world by Mr. R. D. O. Smith and simultaneously by Mr. John Richards in articles published in December, 1893. Among his other inventions, Atkins applied in 1853 for a United States patent on a new form of water-wheel. The patent was not issued until August 10, 1875; and its drawings and specifications show that the inventor had two prime ideas in mind, the minor of which was the building of a wheel containing semi-circular water-ways, of even width and area throughout, and parallel with the axis of the wheel; the water being applied to these buckets simultaneously from a trunk surrounding the wheel. One of the drawings in the Atkins patent is shown in Fig. 1. The major idea of the Atkins patent is that the water in the wheel, as well as the wheel itself, should move at half the speed of the entering water, to facilitate which result, Atkins proposed that the area of the water-way through the wheel should be double the area of the water-way to the wheel. Moreover, his specification declared that, since the peripheral speed of the wheel would be half the velocity of the jet, and since the direction of the jet would be reversed by the shape of the bucket, the water must leave the wheel without velocity, or, in other words, the water should give up all its energy to the wheel.

So far as is known, Atkins never built a wheel upon these principles; but those who know of the serious misfortunes which always pursued him can easily understand why this was never done. The commercial value of the Atkins wheel has, therefore, never been determined. But, while it differed in shape from the present forms of tangential wheels, and had no dividing-wedge in its buckets, it clearly embodied the fundamental principles of the modern tangential wheel, namely, that the water be applied to the periphery of the wheel; that the peripheral velocity of the wheel be approximately one-half of the velocity of the jet; that the direction of flow of the stream be reversed, so that the wheel may absorb the reactive energy of the jet; and that the water leave the wheel without velocity. A significant evidence of the lack of appreciation which American engineers have shown for the value of the Atkins patent is found in the fact that, seven years after it was granted, Messrs. Escher, Wyss & Co., of Zurich, Switzerland, began making water-wheels of the Atkins type, and the practice soon extended all over Europe, especially France. The Atkins type of wheel came back to this country in 1890, however, through the plans for the water-wheels at Niagara, which were made from drawings furnished by Messrs. Faesch & Picard of Geneva, Switzerland, who, with four other European firms, tendered full plans for the construction of these wheels.

Opinions differ as to the relevancy of the Atkins wheel to a discussion of the priority of invention of the tangential wheel; but in view of the plain facts, I must confess my inability to understand any contention that Atkins’ invention has no bearing on that subject. It is true that he neither proposed the use of a split bucket nor suggested that the buckets should enter and leave the stream without shock; nor, indeed, did his wheel have the form or many other features possessed by the tangential wheels of to-day; nevertheless it embodied their basic principles with thoroughness and clearness. The truth of this was recognized in the two articles already referred to. Mr. Smith says:

“ The writer does not propose to discuss the mechanical or theoretical value of this invention further than to suggest that, while, for the enormous pressures under which the Pelton wheel acts, the round nozzle and free jet may be a preferable form, it does not appear to follow that the Pelton wheel is necessarily a more perfect form than the Atkins wheel with its semi-circular buckets, its confined water, and rectangular jets under low pressure. The advantages of the Pelton wheel may be quite dependent upon other considerations, viz., the absence of inclosures and joints capable of withstanding enormous hydraulic pressures, and the absence of friction incident to close fittings capable of withstanding such pressures. It would seem to the writer that the Atkins wheel approaches theoretical perfection as closely as human mechanisms ever approach it, and that the Pelton wheel is a wonderfully successful adaptation of Atkins’ discovery to special circumstances.”

“ In this country the earliest understanding of impulsive action, as distinguished from pressure in turbine water-wheels, seems to have been arrived at by Mr. Jearum Atkins.”

But the Atkins wheel was unknown until the patent was issued in 1875; and in the interim between his application for a patent and its issue, the miners of California had independently developed the “ hurdy-gurdy ” wheel, which, though crude, was the immediate forerunner of the modern type of tangential wheel. The original hurdy-gurdy wheel (named after the musical instrument in which a revolving cylinder takes the place of a fiddle-bow, operating upon strings) resembled a circular-saw with straight-cut teeth more than anything else; the chief difference being that the hurdy-gurdy was made of wood, varying in thickness up to 2 or 3 inches or more. The jet was applied exactly as in present forms of tangential wheels; and the power derived therefrom showed an efficiency of 40 per cent, or thereabouts.

The hurdy-gurdy wheel was made of blocks of wood about 4 inches thick, cut out, as stated, like the teeth of a circular-saw, about 8 inches apart. These teeth or buckets were then closed in by casings of wood which formed the sides of the wheel; and from these sides four arms or spokes were morticed into a log, the end of which was fitted with a round gudgeon for a bearing. The gudgeon was then placed in a live oak block, which had previously been gouged out for the bearing, very roughly, by the way, because of the poor quality of the tools available to the miner of those days. The water was applied at first in the form of a jet, emanating from a hole bored into the end of a wooden block with which the pipe had been plugged. The pipe-line was sometimes of sheet-iron and sometimes of wood. With heads varying from 40 to 50 feet, square wooden pipes were frequently used. These were merely square wooden boxes, bolted together with iron rods, if such could be secured; otherwise the box would be clamped together by means of wooden frames, cleats and wedges.

Such hurdy-gurdy wheels and wooden pipe-lines were considered good practice in 1854; but, as time passed and small quartz-mills were erected, it was found that the sphere of usefulness of the hurdy-gurdy could be enlarged to include the driving of stamp-mills, which it did fairly well, when brass nozzles and moderately high heads were used, as became the common practice. The question of efficiency was not taken into consideration until hurdy-gurdy wheels were applied to the operation of large stamp-mills, when it was found that the hurdy-gurdy would not develop the power required to give the mill the proper speed. This was attributed to the fact that, as the buckets were closed in at each side and on the bottom, the waste-water could not discharge itself freely, and, in consequence, the buckets would remain full during the greater portion of the time they remained in the jet, while all additional water directed against the bucket after it was filled merely slipped over the face of the water already in the bucket. The hurdy-gurdy was a pure impact wheel; and, at that time, little if any thought had been given to the reaction of water as applied to the present forms of tangential wheels.

The gradual evolution of the hurdy-gurdy wheel into the modern tangential wheel was centered in operations mainly confined to Amador and Calaveras counties in California. About 1866 the Pacific Iron-works of San Francisco made a cast-iron wheel to drive a 16-stamp mill at the Gwin mine in Calaveras county, which was the first wheel to embody a material change in the action of the water from that which occurred in the hurdy-gurdy. It had a center-discharge, for the purpose of diverting the direction of the stream, so that the energy which the stream still possessed, after it had lost the portion due to the initial impact could be rendered useful by being guided in a reactive course. The great success of this wheel, as compared with the hurdy-gurdy, proved to be the turning-point in the building of this class of wheels; and it was realized at once that the old hurdy-gurdy had seen its best days.

The next marked improvement was undoubtedly due to Mr. S. N. Knight of Sutter Creek, Cal., who brought out the cup-shaped bucket since universally known as characterizing the Knight wheel. This wheel is of the true tangential type, and its buckets are so shaped that they have both side- and inward discharges, while most of the later types of bucket have mainly side-discharges. The stream of water applied to the Knight bucket is of rectilinear cross-section. The first Knight wheel, made in 1870, presented no radical departure from the present form of the Knight wheel. In 1872 a Knight wheel, placed in the Gwin mine to operate a 20-stamp mill, was first equipped with buckets having an inward discharge; these were then changed so as to have side-discharges; and finally the present form was adopted, which has both inward and side-discharges. This being an important stage in the development of the tangential wheel, it is pertinent to quote the following statement by Mr. Knight concerning the early history of the invention :

“About 1870 I, in common with others, made water-wheels entirely out of wood. The buckets were shaped like saw-teeth, and wooden flanges covered the sides of the buckets, to confine the water; a round nozzle was used; and the general results were considered at that time highly satisfactory. The next step, about two years later, was to make a wooden wheel with iron buckets, giving them a curve and discharging the water toward the center of the wheel—still using, however, the round nozzle.

“Two years later than this, Nicholas J. Colman patented a wheel which had a bucket shaped very much like the present Pelton bucket; the stream splitting and curving off to each side. He, for lack of means, I understand, did nothing with it.

“After two or three years more had passed, I made an improvement by using a curved iron bucket and having the discharge towards the center and to one side, much the same as the Collins (Pacific Iron-works) wheel, still using the round nozzle.

“After continued experiments with the nozzle, Collins found it did not fill the general requirements ; he could not cover enough bucket-space along the periphery of the wheel, without covering an equal space in the width of the bucket, by increasing the diameter of the round nozzle.

“ This induced him to try an elliptical or oblong nozzle ; and the first wheel of this character was placed in the Lamphear mine, at Mokelumne Hill, and it was quickly followed by two others, so satisfactorily did they work.

“From these wheels sprang the present Knight water-wheel; for here it was that I conceived the idea of abandoning entirely any direct modification of the round nozzle, and made the opening a narrow rectangular slit.

“ The round nozzle did well enough where small quantities of water were used ; but upon using considerable water, the nozzle became so large that, while the upper edge could be brought near the wheel the lower edge was far away, and it reduced the power materially ; so the slit was determined upon. More than one nozzle was also tried, but it did not prove satisfactory.

“ In 1875 the first wheel of the present style was placed in the Lincoln mine, at Sutter Creek, and from that time various improvements have been made in the size and arrangement of the slits in the nozzle and shape of the buckets. ’’

We now come to a vexed question, namely, the origin of the jet-splitting wedge. If the records of the United States Patent Office form any criterion, or if after-events of commercial import have any significance, the credit for the wedge-shaped bucket is due to Mr. Nicholas J. Colman of Railroad Flat, Cal. (1873). The specifications of the Colman patent describe a tangential wheel built somewhat after the hurdy-gurdy principle, but with sharply defined buckets containing wedges for dividing the stream. In substance, the specifications describe the action of the water to be as follows: Leaving the penstock, the water strikes the wedge and back of the bucket, exerting its first force upon this back. The wedge divides the water, which then follows the upwardly and outwardly sweeping curve of the discharge-passage, still exerting its force upon the full length of the buckets, while combining its momentum with the centrifugal force acquired by the wheel, and finally discharging at the periphery, through openings which are provided therefor. The two claims of the Colman patent read as follows:

Mr. Knight is my authority for the statement that, to the best of his knowledge, Mr. Colman made a bucket for splitting the stream as early as 1870 ; but so far as Mr. Knight knows, none of the Colman wheels were ever put into use. In any event, it is certain that tangential wheels made under the Colman patent were never brought before the public as a regular manufacture, nor did that patent exert any influence in molding the form of the bucket of the tangential wheel of the present time. It is interesting to note, however, that a few years before the expiration of the Colman patent it was bought from the inventor for $500—which proved to be a very good investment, as the purchaser secured thereby a royalty of $1 for each foot of the diameter of every Pelton water-wheel sold during the life of the Colman patent, upon which basis of settlement he netted about $15,000.

There are several others who claim the invention of the Pelton form of bucket—that is, the bucket containing a dividing-wedge. Among these claimants may be named as prominent Mr. Joseph Moore of the Risdon Iron and Locomotive-works, San Francisco; Prof. F. G. Hesse, Professor of Mechanical Engineering of the University of California; and Mr. L. A. Pelton, inventor of the Pelton water-wheel. According to the statements of these three parties, given below, the divided-wedge form of bucket was invented between 1865 and, say, 1878.

In February, 1897, Mr. Moore issued a monograph in which he claims to be the inventor of the then so-called “ California tangential water-wheel with reaction-buckets.” From 1860 to 1880 Mr. Moore was manager, constructing engineer, director and part owner of the Risdon Iron-works, the records of which institution bear irrefutable support to the statements of his monograph. The substance of this pamphlet, which is quite long, is that in March, 1874, Mr. G. Tiscornia of San Andreas, Calaveras county, Cal., applied to the Risdon Iron-works for information respecting a water-wheel to drive a quartz-mill. After computing the amount of water and head available, Mr. Moore found that it was impracticable to perform the specified work with the hurdy-gurdy wheels then used, in view of which he “ suggested to Mr. Tiscornia a change of buckets, so as to gain reactive effects, also avoid oblique impingements,” further stating that he (Moore) would send Tiscornia a sketch of buckets accordingly. “After some correspondence on the subject,” continues Mr. Moore, “I made, on March 29, 1874, on an order-blank of the Risdon Iron-works, the sketch ” which is reproduced herewith as Fig. 2. On the opposite side of the sheet containing the sketch Mr. Moore wrote a letter to Mr. Tiscornia, dated March 29, 1874, which stated:

“You can see the principle (of the wheel), viz.: to receive the water without shock, at an angle of about 10 degrees, and deliver it at the same, or say 15 degrees. This reaction-water will have no velocity when at proper speed, but will probably react or spout in the opposite direction ; really, its best speed is when it drops straight down, but practically it is best to leave enough velocity in it to clear the wheel.”

“Yours of the 26th just came to hand. Last night I mailed you a sketch of a bucket which I think is quite superior to the one you sketched. It has the same advantages that you expect with yours ; that is, reverses the direction of the water without shock, which is all that can be accomplished by any bucket; but mine has the further advantage of getting rid of the water without its coming in contact with the next bucket, which is a decided advantage, as you see that the water has become stationary with respect to the wheel, or, what is more likely, has got a backward motion ; then the following bucket must impart the velocity of the wheel to the water again, which is just the same as an overshot wheel running in back-water. The proper way is to do the work and get rid of the water, and this, as you see, is accomplished by my bucket, upon which there is no patent.”

The monograph then expresses the opinion that “ not only was the theory (of the tangential wheel) thus laid down, but it was carried out in a manner not since improved upon.”

The order was duly entered in the Risdon order-book, April 7, 1874, for “ a set of hurdy-gurdy wheel buckets, as per pattern and sketch.” The buckets were finished and shipped by express to Mr. Tiscornia on April 13, 1874, and on the same date Mr. Moore wrote to Mr. Tiscornia, saying, among other things :

“You will find, if you let the water play upon the center, that it shoots back with sufficient clearance to free the following bucket. These buckets ought to be 7 to 9 inches apart and the water led on the wheel at an angle not more than 15 degrees, and from a good nozzle, as close up as possible to the buckets.”

In May, 1897, Mr. Pelton published a pamphlet on the “Origin of the Pelton Water-wheel,” containing the following statement, which may therefore be accepted as an authentic presentation of Mr. Pelton’s claims to the priority of invention:

“I crossed the plains from Ohio in 1850, and engaged in mining almost continuously until 1864, when I took up mill-wrighting, in connection with mining, at Camptonville, Yuba county, and other places north of that town, in which business I was employed until 1878; and during this period I constructed a number of water-wheels, of the type commonly known as hurdy-gurdy wheels, having an efficiency of 40 per cent, and upwards, according to the style of buckets used. Here, I conceived, was a chance for improvement ; and early in 1878 I procured the necessary appliances for testing the efficiency of buckets for pressure- or jet-wheels, and devoted most of the time for two years following to designing a bucket which would give a higher efficiency. I tested between thirty and forty different shapes of buckets, and finally noticed that a curved bucket having a jet-strike on the side, as in Fig. 7, instead of in its center (Fig. 6), gave a marked increase in the efficiency of the wheel, but caused an end-thrust against one bearing. To avoid this, I experimented with placing the buckets alternately, as in Fig. 8, when it was but a step to combining the two curved buckets and splitting the stream, as in Fig. 9. This bucket, when tested, gave such astonishing results that I immediately took steps to secure my invention.

“ I introduced my wheel to the public, after obtaining a patent, in October, 1880, and claim to have invented what is known as the ‘ Pelton water-wheel ’ independently, and without any knowledge whatever or aid from the efforts of others in that line.”

This statement is plain, straightforward and convincing; and the writer is but one of many who believe that Mr. Pelton is entitled to the credit he has claimed. Moreover, an analysis of Mr. Pelton’s statement is interesting. In discussing the matter, Mr. Pelton stated to two hydraulic engineers well known to the writer, that at one time, during experiments with a Knight wheel, the key securing the wheel to the shaft loosened, allowing the wheel to become laterally displaced on the shaft, so that the stream of water struck the buckets on their inner side; and that, as a result of this displacement, it was observed that the stamp-mill which the wheel was driving ran faster. This corroborates the statements of Mr. Pelton relative to Figs. 6 and 7, the first of which represents the Knight wheel at that time, while Fig. 7 shows the same bucket as it appeared after the Knight wheel had been displaced, as described. Of course the application of the jet in the manner shown in Fig. 7 would cause an end-thrust against the bearing on the jet-side of the bucket, to obviate which, the alternation of buckets shown in Fig. 8 would naturally suggest itself. As Mr. Pelton says, it would then be but a step in the evolution of the bucket to combine the right and left buckets of Fig. 8 to the simple stream-splitting bucket shown in Fig. 9. It is of further interest to note that the arrangement of the buckets in rights and lefts, as Mr. Pelton states, antedates the distinguishing feature of the Tutthill water-wheel. Moreover, Mr. Knight says that he also experimented on buckets in rights and lefts early in the ’70s, but abandoned the arrangement as being of no advantage to his form of water-wheel.

It seems that Professor Hesse has never made, of his own volition, serious claim to the invention of the divided bucket, but was drawn into the controversy by Mr. Pelton in the hope of disproving Mr. Moore’s contention. The part that Professor Hesse took in the development of the divided bucket appears in a communication to Mr. Pelton dated May 19, 1897, in which Professor Hesse states that some time between 1865 and 1868 Mr. Moore called upon him (Hesse) and asked his advice as to the best water-motor answering the following conditions: high head, good efficiency, and such construction as to admit of its being built of wood at the mill, except flanges, shaft, and such light castings as could be readily transported on pack-animals, Professor Hesse’s reply is best given in his own words :

“ It is clear that, under the above conditions, only those water-motors deserve attention in which the energy of the water to be converted into work is received by the wheel in the form of kinetic energy. The tangential wheel with horizontal axis, a desirable condition, requires to be charged on its inner periphery, necessitating a large angle of entrance (the angle formed by the jet and the tangent to the wheel), causing a diminished efficiency and entailing, on account of limited space, a more costly construction. A wheel of the Jonval type with horizontal axis, the water flowing in planes parallel to the axis, seemed to answer best. It has, however, the disadvantages of being unbalanced: a serious point, considering the ever-shifting movement about the center, great number of revolutions, and large radius. Adding to this the necessity for a great number of buckets, with great length of water-way, to cause a proper discharge between the limited angles of entrance and discharge, it is clear that such a wheel would be heavy and of costly construction. I was aware of the fact that two such wheels, mounted on the same shaft, had been used heretofore to balance (see Fig. 10). Then it occurred to me that two such wheels might be placed together, so as to form one wheel, and one bucket out of every pair of buckets, reducing thus the entrance angle to 0, causing an increase of efficiency (Fig. 11). The jet entering in a direction tangential to the wheel is divided and discharges in two streams at the opposite sides of the wheel. Another advantage is to be found in the increased passage-way of the discharge-water, one on each side of the bucket, a fact which greatly lessens its weight and facilitates its free discharge. The best form of bucket could only be determined by actual tests and experiments, which were not made for lack of time. I furnished drawings for such a bucket to Mr. Moore, and was afterwards informed by him that castings were made from this design, and were sent to a mine to be bolted to the rim of a wooden wheel. The result of the performance of the wheel, provided it was built, never reached me. Having never contemplated taking out a patent for what I considered so obvious an improvement, I lost sight of the matter from that time.”

The writer is therefore convinced that Mr. Moore and Professor Hesse were the first to suggest the generally adopted form of the tangential-wheel bucket, containing the dividing- wredge to direct the flow of the water in reversing its direction.

But the statements of these three highly respectable men are given especially to show that different minds were working simultaneously upon the same problem. Did time and space permit, the efforts of many others in the same direction could be similarly detailed, conclusively demonstrating that the evolution of the tangential water-wheel bucket has had a history in which have figured not only the names of Atkins, Knight, Colman, Moore, Hesse, Tiscornia and Pelton, but also, and largely coincident with them, those of James Patterson, Louis Biggio, John B. Pitchford, S. L. Berry, Francis M. F. Cazin, Daniel Hug, W. G. Dodd, the Risdon Iron-works (San Francisco), and the early wheels of D. Donnelly of Sutter Creek, and Watson of Nevada City, Cal., as well as James Leffell & Co., the Risdon Iron-works, and the Abner Doble Co., with their respective Cascade, Risdon and Ellipsoidal wheels respectively. Still other wheels might be mentioned, such as the Kale, Ridgway, Bookwalter and Tutthill. The forms of the Pelton and Dodd buckets are shown in Figs. 12 and 13 respectively.

Of these buckets, the Biggio is the only one that does not claim distinct advantages from the use of a sharp central and radial division which splits the stream. In the Biggio bucket, which is shaped something like the letter “ W,” made with low rounded turns instead of angles, the central ridge is but a partial division. The Pitchford bucket contains a sharp, radial dividing-wedge, and the front or outer lip of the bucket slopes towards the direction of rotation, so as to prevent this outer lip from striking the jet when the bucket enters the stream. This patent also provides a means whereby “the true apex of the bucket” may be centered in the stream. The Berry patent (Fig. 15) contemplates a divided bucket of such shape as to present, in the plane of rotation, surfaces at right-angles with the stream, permitting a free discharge tangential to the wheel, and avoiding disturbance of the stream on entrance. This the patentee endeavors to obtain through the use of convex instead of concave surfaces for the faces of the buckets which are presented to the jet. The Cazin patent partakes of Pitchford’s idea, in that its bucket is intended so to enter the jet as to prevent the slapping of the stream by the lip of the bucket. Cazin professes to accomplish this by projecting the peripheral lip or edge, still using radial wedges (as do all buckets other than the ellipsoidal, which will be described later). The Cazin bucket divides the stream in two entirely distinct planes, viz.: first in a plane parallel to the axis of the wheel’s rotation, and, second, in a plane at right-angles thereto, or in the plane of the wheel’s rotation. The Cazin wheel, moreover, is so designed that the entering lip, which is transverse to the plane of rotation, first enters the stream, but the end of this entering lip travels a path of greater radius than that which is covered by the bucket proper; therefore as soon as it enters the stream the jet is deflected, so that it misses the bucket next in advance of the entering one. Cazin thus not only loses the direct effort of the stream, but, by missing that bucket entirely, the possible reactive effect of the water thus deflected is lost. The same is true, however, in smaller degree, of practically all the other types of buckets having straight entering lips, as will be more fully shown further on. The Pelton, Risdon, Hug, Cazin and Dodd buckets are characterized by the broad edge which forms the entering lip of the bucket. This lip, in conjunction with the splitting-wedge, exerts a twofold influence upon the stream; first, the entrance of the bucket into the jet causes the stream to be split by the entering lip in a plane that is axial to the wheel; secondly, as the portion of the jet which is diverted into the bucket encounters the splitting-wedge therein, the water is again divided, and, instead of pursuing its natural flow, is ordinarily forced to follow a path provided for it. These lipped buckets are, therefore, objectionable in several respects. They not only divert the stream from its natural course while the lip is passing through the stream, but they also break up that part of the stream which is entering the buckets, setting up in the water a violent swirling action, which prevents its smooth flow through the buckets. This not only cuts the buckets, but also destroys the best results of reaction of the water, and causes an additional loss of efficiency through the reaction of part of the discharged water against the back of the next following bucket (see Fig. 14). The Dodd bucket, which has been acquired by the Pelton Water-wheel Co. and, in a slightly modified form, is gradually displacing the original form of Pelton bucket for high heads (the form always meant in this paper when the “ Pelton ” bucket is named) partly obviates the inherent disadvantages of the straight-lipped bucket by giving the entering lip a curved-in form, which more quickly envelopes the stream than it is possible to do with a straight edge. The Ridgway, Bookwalter, Kale, Watson, Tutthill and Cascade wheels form a class by themselves, in that the buckets are placed alternately on the sides of the wheel rim, that is in rights and lefts. Ridgway placed two directing ribs equi-distant through the radial line of the bucket, the shape of which bears a strong resemblance to the cups used on belt elevators for hoisting grain. The Bookwalter bucket had a simple cup-shape, and was so arranged on the periphery of the wheel that but half of the jet

entered each bucket; that is, the inner edges of the alternate buckets did not overlap. The difference between the Book- walter and the Tutthill wheel, therefore, rests mainly in the fact that in the Tutthill wheel the entire jet as a unit goes into the buckets. In the Watson, Kale and Cascade wheels, the central dividing edge is placed around the periphery of the wheel, in the plane of its rotation, and central to the jet; and on the opposite sides of this dividing edge the buckets are placed in rights and lefts. In the Kale wheel the buckets are but straight paddles as in the familiar flutter-wheel, while the other wheels use cup-shaped buckets.

An ideal bucket for a tangential water-wheel, that is, a bucket from which would be secured the greatest effective power for the energy applied, would receive the stream of water in a solid condition, reverse its direction without breaking it up into spray, and discharge it along natural lines in an even flow over the whole bucket-surface. Its form would be such that the plane of the bucket, say, at the edge of the dividing-wedge, would always be perpendicular to the direction of the stream. Finally, the force exerted by impact and reaction from the stream would be equal, whatever angle the plane of the bucket might bear to the axis of the jet. Of course every effort should be made to minimize the friction between the stream and the surface of the bucket (a principle opposed to the idea which prevailed in the design of the Biggio bucket); to give ample clearance between the buckets, that they may discharge freely; to give each bucket the longest possible arc of contact with the stream; to avoid beating or slapping the stream with the lips of the buckets ; and so to dispose the buckets that each, as a whole, will enter and leave the stream with the utmost quickness.

The buckets of the most familiar forms split the stream on entering it, in two planes, viz.: the entering lip splits in the plane transverse to the wheel’s rotation, while the dividing-wedge in the center of the bucket splits the stream in the direction of the wheel’s rotation. The transverse splitting is both unnecessary and undesirable. A bucket which will not split the stream transversely, and which is of such a shape as to preserve the perpendicular position relative to the stream above specified, is found in the ellipsoidal type, which has no entering lip, and the shape of which is described from true hydraulic curves. Interesting illustrations of the above propositions are furnished by buckets taken from wheels which have been run with water containing sand, grit or “ slickens.” One of them, of the Pelton type, is shown in front and back views, respectively, in Figs. 22 and 23. Under these conditions, the faces of the buckets are badly worn from striking against the jet; the corners within the buckets are deeply cut or perforated, according to the time of service (in this case, 8 weeks); and the inner corner of the back of each bucket, is similarly worn and perforated from the backward discharge of the immediately preceding bucket. These erosions are all due to the swirling of the water because the bucket is so formed as to prevent proper discharge. The reason will be clear from an examination of Fig. 14. The jet, striking on the inner side of the face of the bucket, glances off the surface at an angle equal to that of incidence; and this action occurs at three points within the bucket, namely, on its front, bottom and rear faces, as is clearly shown by lines of erosion cut by the sediment carried in the water. As an inevitable consequence, a swirling action will take place at the corners f, g and h,Fig. 14, resulting in great loss of energy and the eventual perforating of the bucket at these points.

Buckets made on true hydraulic lines show no pitted erosion; such wear as occurs in them is uniform and even throughout. Figs. 30, 31 and 32 represent an ellipsoidal bucket which has been in continuous service for twelve months under a head of 400 feet at the Dreisam mine, W. Moorehead, Superintendent, Soulsbyville, Tuolumne county, Cal. Here the water contains much grit; from 2 to 3 tons of sand per day passing through the pipe-line and being shoveled out from the tail-race daily. Fig. 30, a face-view, shows the smooth uniform wear on the active and reactive faces of the bucket, which are entirely free from erosions such as would occur from swirling water. This also indicates a uniform discharge of the water around the entire discharge-edge of the bucket. Fig. 31, likewise a face-view, shows the wear on the dividing-wedge, which, being greatest at the middle of the bucket, demonstrates that the maximum effort of the water is at this point, where it would produce the best results. Fig. 32 is a back-view of the same bucket, showing absolute freedom from any impingement of the water on the back of the bucket, the skin of the casting remaining as it originally left the mould. The smooth wear of this bucket, with the total absence of any eddy-action, is believed to prove the correctness of the hydraulic curves, and likewise of the theories on which the design of the bucket is based. Note in Figs. 30 and 31 the slight depression in the center of each bowl of the bucket. This depression is directly opposite the reinforcing ribs on the back of the bucket (see Fig. 32); and the additional wear at this point was caused by the difference in the hardness of the casting. The metal where the reinforcing rib joined the bucket, having more body, cooled more slowly in the mould than the other and thinner parts of the bucket, causing the metal at this point to be slightly softer; whereas the iron in the thin section of the bucket showed a tendency to chill, and thus permit the greater erosion at this point. The shape and location of this depression clearly prove this.

To appreciate these points fully, it must be borne in mind that, unless the stream enters the buckets from their sides, simple cup-shaped buckets, without dividing-wedges, permit the accumulation of dead water at the base of the cup. The splitting-wedge was devised to do away with this dead-water, and to extend an invitation to the live water to turn its direction back upon itself, that it might, by reaction, impart further energy to the wheel. The invention of the dividing-wedge, therefore, constituted a long step in the right direction. Again, the maximum torque which a tangential wheel, held stationary, will exert, will be given when the direction of the jet is, as stated, perpendicular to the plane of the bucket; that is to say, the angle of the maximum effort which a jet can exert is tangential. There are two ways by which this condition may be satisfied, one of which is impracticable, while the second is simple and effective. The feathering paddle-wheel offers the key to the first solution, for, as it always enters the water at right-angles, it would keep the plane of a water-wheel bucket perpendicular to the axis of the stream during the arc of contact. But the application of this device to tangential wheels, with their high rotative speeds and centrifugal force, presents mechanical difficulties which preclude all hope of success. The second solution is found, deeply veiled, in the Berry bucket (Fig. 15), the reciprocal of which furnishes such hydraulic curves for the faces of buckets as will give a smooth and uniform distribution of forces over practically the entire surface of the bucket, regardless of its position in the arc of contact with the stream. This feature is more fully developed in the ellipsoidal type, to be further discussed below.

The ideal bucket should possess some other important features. The manner in which the jet is brought into contact with the bucket is of paramount importance. All will concede that the stream should enter the bucket in a solid condition; in other words, it should be disturbed in the least possible degree. The entrance lips in use are either straight or in-curved. The great majority of buckets have the straight lips as in the original Pelton, the Risdon, Hug, Cazin and other well-known forms. The main example of the curved entrance lip is found in the Dodd wheel. The ellipsoidal bucket has no entering lip. I cannot but believe that, of the two latter, the last is the more efficient, for the reason that the Dodd bucket is so formed that the stream is split, before entering the bucket, by the in-curved lip, while in the ellipsoidal bucket the solid stream is not split or otherwise interfered with, in any manner whatever, until after it meets the dividing-wedge.

In fact, the only contact of the ellipsoidal bucket on entering the stream is with the dividing-wedge. A lipped bucket tends to break up the stream and to deflect it during the transit of the lip, thus setting up swirling actions which interfere seriously with the reactive effect. It tends, moreover, to divert the stream outwardly, because of splitting it as by a wedge having an edge which is axial to the wheel; and thus it splits the stream transversely (see Fig. 14) before the wedge in the bucket has an opportunity to split it radially to the wheel and reverse the direction of the water. Finally, in the ellipsoidal bucket the stream is only divided in the plane of the wheel’s rotation, and thus separated into only two equal parts, each of which flows over the hydraulic-curved faces in the bucket, reversing the direction of flow without disturbance of shock, and avoiding the eddy-currents set up where an end lip is used. Buckets of the entering lip type first shave off the stream in thin slices, each slice being again divided by the central dividing-wedge, this additional disturbance to the stream preventing the smooth flow of the water through the bucket, which is essential to high efficiency.

The condition which the ideal bucket imposes, that the water shall follow along natural lines and receive an even flow throughout the whole surface of the bucket, is one which has not been satisfied by any of the forms of tangential wheels with which the engineering public is most familiar. Proof of this, as already observed, will be found in a study of buckets of those makes that have been in use for some time under high heads of water containing slickens or sand. Such buckets as those illustrated in Figs. 16 to 22 inclusive, show strongly marked erosions from whirling water within them, and demonstrate that nature often ignores entirely those paths which the designers of the buckets had selected as proper directions of discharge, and that the water takes a radically different course therefrom, as is proved by the erosion. In some cases of operation under comparatively moderate heads, this erosion is so great in the best known type of bucket as to perforate the bucket in from six weeks to two months, requiring new buckets throughout the wheel. One of these perforated buckets is shown in Figs. 22 and 28.

In Fig. 16 (Pelton bucket) the perforation and erosion at the junction of lip and bucket-face may be noted. In Fig. 17, a small bronze Dodd bucket has its face or outer surface so formed that, in dividing the stream approximately at right-angles to the plane of rotation, it continually strikes the stream with this outer face, as is evidenced by much wear, and a perforation which can be clearly seen thereon. Such evidence demonstrates that there is a retarding influence to the passing of the buckets into the stream, as will appear on examination of Fig. 18. If we consider this in connection with the fact that the wheel from which the bucket shown in Fig. 17 was taken contained forty such buckets and ran at about one thousand revolutions per minute, giving, therefore, forty thousand impacts or disturbances per minute to the stream, we can appreciate the fact that this continual slapping in the stream would necessarily have a tendency to seriously break it up. More than this, it deflects the stream so that much of it entirely misses the bucket in advance of the bucket entering the stream (see Fig. 14).

In Fig. 18, the inner surface of a Dodd bucket is also much eroded in such a way as to disprove the theories formerly advanced concerning the discharge of water from buckets of this type. The erosion in this case shows conclusively that the greater discharge of water was from the upper and lower corners, or the inner and outer ends of the buckets; in fact, one outer end of the bucket shown in Fig. 17 is entirely cut through, while the side of the bucket whence the discharge was supposed to have taken place shows no appreciable wear, but retains practically its original thickness. The metal is also very much worn away from the inner to the outer end of the bottom of the bucket. Fig. 21 shows the whirlpool-action of the water in a modified Dodd bucket. These erosions, and the others shown, were clearly due to violent whirlpools in the water, and demonstrate that the lower end of the bucket divides the stream into horizontal strata, so as to break up and destroy its solid condition. Instead of the bucket being acted upon by solid water, it is therefore in reality filled up with a swirling mass, which causes the loss of the best effects of reaction, and reduces the efficiency very materially. Such specimens of worn water-wheels are by no means rare. As a rule, the sides which are supposed to form the discharging- or reacting-faces show very little, if any, wear, while the bottoms and ends, and particularly the corners, show the most wear, and often complete perforation, as the effect of the eddying currents (see Fig. 18). In the Dodd bucket, shown in Fig. 19, the outer lip is much worn from striking the stream; whereas the inner surface of the lip shows no wear whatever, although directly on the other side of the wall from the preceding. The conclusion is inevitable that, had the end of this bucket been left open, the energy of the water which was wasted in wearing the outer end would have given useful effect on the reactive faces, to say nothing of the advantage that would have followed from not breaking up the stream many thousand times per minute.

It is worth noting that the builders of these wheels designed the curves and shapes of the buckets with the wheel stationary, and did not take into consideration its relative velocities and the resulting angles of the buckets to the impinging jet. This is shown by the fact that all existing drawings detailing the application of the jet to the bucket show the jet impinging in the middle of the bucket, and divided into two semi-circular sectional streams of water, flowing over the faces and discharging from the sides of the buckets. The divided water is shaded in such drawings, to indicate its semi-circular section, whereas in reality the impingement of a stream of water against a surface or inclined plane causes the water to flatten and spread. This condition not being taken into consideration, the designers overlooked the requirements of free discharge. In reality, the buckets move rapidly in relation to the stream ; but in designing the curves of the buckets they have considered the actions and reactions of the stream within the bucket to be the same as if the bucket were stationary. On the contrary, the problem of the resolution of forces of the tangential wheel changes with each and every change in the position of the bucket with reference to the stream. The first authentic record of a thorough appreciation of these variations in forces which result with each change in the position of the wheel appears in the Berry patent (1893). If it be granted, as perhaps it may be, that some of the buckets produced by well-known manufacturers are correctly designed as to impulse and reaction at one given point of impingement—say, when the axis of the stream is perpendicular to the plane of the base of the bucket— then it unquestionably follows, from the equally indisputable fact that this angle and the bucket-curves are constantly changing during the period of contact between stream and bucket, that the design of the bucket, when in all other positions than that of the perpendicular stated, must vary correspondingly from a condition of slight error to one of absolute wrong. So marked is this error, that one who studies the situation in all of its many phases can but wonder that the most familiar types of tangential wheels embodying these defects in design should be possessed of a laboratory-efficiency of over 70 per cent, (which, however, they seldom realize in actual practice). The idea which prevailed in the design of the Berry bucket was, that the axis of the stream should be normal to the surface of the bucket, whatever its position within the arc of contact with the stream. To accomplish this, buckets of convex forms, of a carefully calculated curvature, were used. Just why this bucket has never seen commercial usage (unless it be that it has gone the way of many other good and useful inventions, and has been “ shelved ” by its owners) is not apparent at first; but becomes so on reflecting that, while the axis of the stream may be perpendicular to the tangent of the surface of the bucket, the stream itself, having breadth and consequently bulk, can never be such. In other words, the axis of the stream is an imaginary line without cross-section ; the stream has cross-section ; hence the line forming an outer confine to the stream, though parallel with the axis, will not be normal to the surface of the bucket. Herein rests the vital point pertaining to the Berry bucket in a commercial sense—the theory of the bucket is correct, but practically it is without distinguished utility, for the reason stated.

The theoretical feature of the Berry bucket which has been discussed, marked a distinct innovation in water-wheel practice, when its inventor declared that “ a thin edge entering the stream transversely is better than any entrance made at an angle (i.e., as in the Risdon, Pelton, Hug, Dodd, Cazin, Tutthill and Cascade buckets) or any of the forms hitherto adopted, because not only must disturbance be taken into account, but also the effect produced by the diverted water while the stream is being severed. (See Fig. 14.) The two things must be considered together; the value or effect of disturbance is much more complex than the losses due to misdirected water.” In this Mr. Berry was quite correct; but, to go a step further, it is obvious that if the transverse splitting of the stream could be avoided, that is, if the bucket could enter the jet without splitting it transversely; if the first and only splitting of the stream could be that caused by the radial dividing-wedge within the bucket; and if the curvature of this bucket could be such that the resolution of the forces exerted by the stream would always be in lines tangential to the surface of the dividing-wedge, whatever be its position in the arc of contact with the jet, then the highest possible efficiency will have been attained. These revolutionizing features are accomplished by the new form of ellipsoidal bucket, which has been brought out within the past year. The writer is therefore constrained to say that the latest and most important change and improvement in tangential water-wheel practice, since the development of the Colman-Moore-Heese buckets, has been the recent adoption of what may be called true hydraulic curves for the faces of the buckets, and the division of the jet vertically, or radially and in one plane only, after its entrance within the bucket.

The first of these features has, by some strange oversight, escaped the attention of engineers. For fifty years past it has been a prominent and even essential feature in turbine-practice, and indeed in all of the refined type of water-wheels wherein the water was reversed in its course over the faces of the buckets; but it has not been considered, or at least has not been applied, in tangential-wheel practice, up to the time when the buckets shown in Figs. 24 to 28 were adopted for wheels installed for operation in large units under high head. Previously the faces of the buckets had either been true curves, or developed curves that did not conform to the hydrodynamic conditions demanded.

“ The buckets are of a double-trough form, having an elliptical contour, as shown in Fig. 24, the transverse curves at the center terminating in an acute wedge E that splits or divides the stream C into two equal parts that are diverted by this wedge, and the curves at its sides each way into the troughs forming the sides of the bucket. The form of the buckets in two planes is indicated in Figs. 25 and 26, the face or rim in Fig. 24 presenting ellipsoids developed from radii approximately, as shown, so that the curves traversed by the water after its impingement are the same in whatever direction it may flow after impingement.

‘‘ In my former application for letters-patent, the buckets, while the same in general construction and disposition as those herewith illustrated, were formed with straight sides and bottoms, and with true curves only, so the water preserved during its flow over such surfaces a uniform velocity. Subsequent experiments proved that a greater efficiency could be obtained by means of modified curves of an ellipsoidal form, as herewith illustrated, and known as the hydraulic curves for such surfaces.

“This ellipsoidal form of the acting surfaces which guide the flow of water in the buckets produces, as will be seen, a cumulative degree of deflection until the direction of flow is reversed—maintaining the velocity of the water with the least retardation and thus securing the maximum reactive effect, avoiding irregular flow and gaining a complete clearance of the water from the bucket after its energy is expended, also permitting a greater velocity of the wheel-rim in proport