wire rope calculation formula for sale

Structural Stretch is the lengthening of the lay in the construction of cable and wire rope as the individual wires adjust under load. Structural Stretch in Loos & Co., Inc. products is less than 1% of the total cable length. This form of stretch can be completely removed by applying a cable or wire rope prestretching operation prior to shipment.

Elastic Stretch is the actual physical elongation of the individual wires under load. The elastic stretch can be calculated by using the following formula*:

Wire ropes are essential for safety purposes on construction sites and industrial workplaces. They are used to secure and transport extremely heavy pieces of equipment – so they must be strong enough to withstand substantial loads. This is why the wire rope safety factor is crucial.

You may have heard that it is always recommended to use wire ropes or slings with a higher breaking strength than the actual load. For instance, say that you need to move 50,000 lbs. with an overhead crane. You should generally use equipment with a working load limit that is rated for weight at least five times higher – or 250,000 lbs. in this case.

This recommendation is all thanks to the wire rope safety factor. This calculation is designed to help you determine important numbers, such as the minimum breaking strength and the working load limit of a wire rope.

The safety factor is a measurement of how strong of a force a wire rope can withstand before it breaks. It is commonly stated as a ratio, such as 5:1. This means that the wire rope can hold five times their Safe Work Load (SWL) before it will break.

So, if a 5:1 wire rope’s SWL is 10,000 lbs., the safety factor is 50,000 lbs. However, you would never want to place a load near 50,000 lbs. for wire rope safety reasons.

The safety factor rating of a wire rope is the calculation of the Minimum Break Strength (MBS) or the Minimum Breaking Load (MBL) compared to the highest absolute maximum load limit. It is crucial to use a wire rope with a high ratio to account for factors that could influence the weight of the load.

The Safe Working Load (SWL) is a measurement that is required by law to be clearly marked on all lifting devices – including hoists, lifting machines, and tackles. However, this is not visibly listed on wire ropes, so it is important to understand what this term means and how to calculate it.

The safe working load will change depending on the diameter of the wire rope and its weight per foot. Of course, the smaller the wire rope is, the lower its SWL will be. The SWL also changes depending on the safety factor ratio.

The margin of safety for wire ropes accounts for any unexpected extra loads to ensure the utmost safety for everyone involved. Every year there aredue to overhead crane accidents. Many of these deaths occur when a heavy load is dropped because the weight load limit was not properly calculated and the wire rope broke or slipped.

The margin of safety is a hazard control calculation that essentially accounts for worst-case scenarios. For instance, what if a strong gust of wind were to blow while a crane was lifting a load? Or what if the brakes slipped and the load dropped several feet unexpectedly? This is certainly a wire rope safety factor that must be considered.

Themargin of safety(also referred to as the factor of safety) measures the ultimate load or stress divided by theallowablestress. This helps to account for the applied tensile forces and stress thatcouldbe applied to the rope, causing it to inch closer to the breaking strength limit.

A proof test must be conducted on a wire rope or any other piece of rigging equipment before it is used for the first time.that a sample of a wire rope must be tested to ensure that it can safely hold one-fifth of the breaking load limit. The proof test ensures that the wire rope is not defective and can withstand the minimum weight load limit.

First, the wire rope and other lifting accessories (such as hooks or slings) are set up as needed for the particular task. Then weight or force is slowly added until it reaches the maximum allowable working load limit.

Some wire rope distributors will conduct proof loading tests before you purchase them. Be sure to investigate the criteria of these tests before purchasing, as some testing factors may need to be changed depending on your requirements.

When purchasing wire ropes for overhead lifting or other heavy-duty applications, understanding the safety dynamics and limits is critical. These terms can get confusing, but all of thesefactors serve an important purpose.

Our company has served as a wire rope distributor and industrial hardware supplier for many years. We know all there is to know about safety factors. We will help you find the exact wire ropes that will meet your requirements, no matter what project you have in mind.

Wire rope and chain are the important part of the hoist which are closely bound up with the safe work load, now let’s talk about how to calculate the SWL of ropes and chains.

Sticking on national standards, DQCRANES has passed ISO9001 international quality system certification, ISO14004 environment management system certification, OHSA18001 and European CE Certifications which comprehensively promotes overall management level and makes DQCRANES known and welcomed by international customers.

Rope strength is a misunderstood metric. One boater will talk about tensile strength, while the other will talk about working load. Both of these are important measurements, and it’s worth learning how to measure and understand them. Each of these measurements has different uses, and here we’re going to give a brief overview of what’s what. Here’s all you need to know about rope strength.

Each type of line, natural fiber, synthetic and wire rope, have different breaking strengths and safe working loads. Natural breaking strength of manila line is the standard against which other lines are compared. Synthetic lines have been assigned “comparison factors” against which they are compared to manila line. The basic breaking strength factor for manila line is found by multiplying the square of the circumference of the line by 900 lbs.

When you purchase line you will buy it by its diameter. However, for purposes of the USCG license exams, all lines must be measured by circumference. To convert use the following formula.

As an example, if you had a piece of ½” manila line and wanted to find the breaking strength, you would first calculate the circumference. (.5 X 3.14 = 1.57) Then using the formula above:

To calculate the breaking strength of synthetic lines you need to add one more factor. As mentioned above, a comparison factor has been developed to compare the breaking strength of synthetics over manila. Since synthetics are stronger than manila an additional multiplication step is added to the formula above.

Using the example above, letÂ’s find the breaking strength of a piece of ½” nylon line. First, convert the diameter to the circumference as we did above and then write the formula including the extra comparison factor step.

Just being able to calculate breaking strength doesn’t give one a safety margin. The breaking strength formula was developed on the average breaking strength of a new line under laboratory conditions. Without straining the line until it parts, you don’t know if that particular piece of line was above average or below average. For more information, we have discussed the safe working load of ropes made of different materials in this article here.

It’s very important to understand the fundamental differences between the tensile strength of a rope, and a rope’s working load. Both terms refer to rope strength but they’re not the same measurement.

A rope’s tensile strength is the measure of a brand-new rope’s breaking point tested under strict laboratory-controlled conditions. These tests are done by incrementally increasing the load that a rope is expected to carry, until the rope breaks. Rather than adding weight to a line, the test is performed by wrapping the rope around two capstans that slowly turn the rope, adding increasing tension until the rope fails. This test will be repeated on numerous ropes, and an average will be taken. Note that all of these tests will use the ASTM test method D-6268.

The average number will be quoted as the rope’s tensile strength. However, a manufacturer may also test a rope’s minimum tensile strength. This number is often used instead. A rope’s minimum tensile strength is calculated in the same way, but it takes the average strength rating and reduces it by 20%.

A rope’s working load is a different measurement altogether. It’s determined by taking the tensile strength rating and dividing it accordingly, making a figure that’s more in-line with an appropriate maximum load, taking factors such as construction, weave, and rope longevity into the mix as well. A large number of variables will determine the maximum working load of a rope, including the age and condition of the rope too. It’s a complicated equation (as demonstrated above) and if math isn’t your strong point, it’s best left to professionals.

However, if you want to make an educated guess at the recommended working load of a rope, it usually falls between 15% and 25% of the line’s tensile strength rating. It’s a lotlower than you’d think. There are some exceptions, and different construction methods yield different results. For example, a Nylon rope braided with certain fibers may have a stronger working load than a rope twisted out of natural fibers.

For safety purposes, always refer to the information issued by your rope’s manufacturer, and pay close attention to the working load and don’t exceed it. Safety first! Always.

If you’re a regular sailor, climber, or arborist, or just have a keen interest in knot-tying, be warned! Every knot that you tie will reduce your rope’s overall tensile strength. Some knots aren’t particularly damaging, while others can be devastating. A good rule of thumb is to accept the fact that a tied knot will reduce your rope’s tensile strength by around 50%. That’s an extreme figure, sure, but when it comes to hauling critical loads, why take chances?

Knots are unavoidable: they’re useful, practical, and strong. Splices are the same. They both degrade a rope’s strength. They do this because a slight distortion of a rope will cause certain parts of the rope (namely the outer strands) to carry more weight than others (the inner strand). In some cases, the outer strands end up carrying all the weight while the inner strands carry none of it! This isn’t ideal, as you can imagine.

Some knots cause certain fibers to become compressed, and others stretched. When combined together, all of these issues can have a substantial effect on a rope’s ability to carry loads.

Naturally, it’s not always as drastic as strength loss of 50% or more. Some knots aren’t that damaging, some loads aren’t significant enough to cause stress, and some rope materials, such as polypropylene, Dyneema, and other modern fibers, are more resilient than others. Just keep in mind that any knots or splices will reduce your rope’s operations life span. And that’s before we talk about other factors such as the weather or your rope care regime…

With nearly 4,000 employees worldwide, WireCo WorldGroup is a great place for you to build a rewarding career. Our professionals enjoy the opportunities of a global manufacturing and distribution leader as well as a culture of open communication, professional growth, and friendly camaraderie that fosters innovation and problem solving.

Enter the diameter of the wire rope, in mm, into the calculator to determine the safe working load (SWL). This calculator is for education purposes only, follow manufacturing guidelines for true SWL values.

A safe working load of a wire rope is a measure of the total load or weight that a wire rope can safely support during operation. Values greater than the SWL could result in a failure of the rope.

After determining the correct size wire rope or cable, many think they have taken all the necessary steps to buy the right product for their application. However, this is not the case! A commonly overlooked, but highly important factor when purchasing cable and wire rope is stretch. It is crucial to know about the two types of stretch (Structural and Elastic) and the formula for calculating stretch in cable. Continue reading to learn about the importance of stretch and how it is determined to ensure you get the right wire rope and cable for your application.

Structural stretch is the lengthening of the lay in cable and wire rope construction as the individual wires adjust under load. While certain levels of this stretch may be required, it is possible for stretch to be entirely removed by applying a pre-stretching operation to cable or wire rope before shipment.

Elastic stretch is the elongation of individual wires under load. The elastic stretch of cable or wire rope can be determined by using the formula below:

To calculate stretch, a formula can be applied. The formula is (E= (W x G) / D2). The values derived from this calculator are an approximation, and it is important to remember to keep your units of measure constant. The most common measurement for cable is inches.

While weight and diameter are simple to determine, Stretch Factor (G) is a bit trickier. Thankfully, Strand Core provides a visual guidewith different stretch factors for various wire rope constructions. For example, 1x7 302 SS wire rope has a stretch factor (G factor) of 0.0000735 while 1x7 Galvanized wire rope has a G factor of 0.00000661. Another example is 1x19 302 SS wire rope has a G factor of 0.00000779, and 1x19 Galvanized wire rope has a G factor of 0.00000698. To find the G factor of 7x7, 7x19, 6x19, 6x37, and 19x7 constructions, you can visit our guide here.

By understanding the two types of stretch and the formula for calculating stretch, you will know exactly how much stretch occurs in your cable or wire rope application. Even though it may seem daunting at first, determining the stretch for cable or wire in applications is critical in choosing the suitable cable or wire for the job, and it"s easy with our helpful guides!

If you are looking for a place to buy wire rope or cable, look no further than Strand Core. Why buy with us? We carry various styles and sizes of cable and rope, our products are Manufactured in USA, and we can provide a custom configuration of materials and constructions that comply with various industry specifications. If you want to learn more, please visit our website here. If you have any questions, our team is happy to help! Reach out to us by email through sales@strandcore.com or by phone at 800-983-9926.

Have you ever wondered how much weight a wire cable can safely hold? It’s surprising how strong wire cables are. Although wire cables often have small diameters and look flimsy, their strength is impressive. Calculating how much weight a wire cable can hold is called a Safe Working Load (SWL), and involves a mathematical formula. The SWL is usually calculated by the manufacturer of the cable and is marked on the packaging to inform consumers. To ensure your safety, always take note of the SWL the manufacturer provides.

SWL can also apply to other lifting devices or components of lifting devices, such as a line, rope or crane. The SWL is also sometimes referred to as Normal Working Load or Working Load Limit. It is the mass that lifting equipment can safely hold without fear of breaking. The SWL or NWL is often a fifth of the Minimum Breaking Strength of the cable, although sometimes other fractions are used, depending on the manufacturer.

To calculate the SWL, you need to know the diameter of the cable or rope. While you may find this on the packaging, you can also calculate it manually by measuring it yourself. Ensure that you enclose all of the strands of rope when measuring the diameter, and measure from the top of one strand to the top of the strand which is directly opposite. If you’re worried about the accuracy of your measurements, conduct your measurements three times at different places on the cable, and use the average of your three measurements as the diameter of the rope.

Once you know the diameter of the rope, you can apply it to the formula, which is SWL = D2 x 8. D represents the diameter of the rope in inches. If you’re working with a 1.5-inch diameter cable, for example, then the formula would be SWL = 1.52 x 8 or SWL = 2.25 x 8. This calculation means the SWL of a 1.5-inch diameter rope is 18 tons.

Take note that most manufacturers will provide you with the SWL for their rope or cable under specific conditions. It’s important to use the SWL the manufacturer gives you. If you’re working with old rope or rope that is worn down, you may want to reduce the SWL of the rope by as much as half, based on the condition of the rope. You can also use the manufacturer’s Breaking Strength of the rope if it is available.

Ropes come in many different diameters and there are guidelines to help you choose the right diameter for your purpose. But how do you know which diameter the halyards and sheets on your boat are? How do you measure the diameter?

The diameter of a rope is based on the combination between the construction of the rope and the amount of material used. A rope can be heavy and compact, or light and loosely braided. This influences the properties of the rope and therefore can affect the measurement of the size. A loosely braided rope gets thinner and flattens out under load, whereas a compact rope with more fibres will keep its shape. This is why measuring the diameter when the rope is under load will have different result as to when the rope is not loaded.

Due to this, the diameter of rope is less precise than with steel wire. Determining a diameter for ropes is an empirical process. This means that every manufacturer develops and adapts a rope, based on observation and experience. This causes the possibility for small differences between ropes with, according to the specification, the same diameter. A rope that is specified as a 10mm rope can therefore sometimes be 9mm or in other cases 11mm.

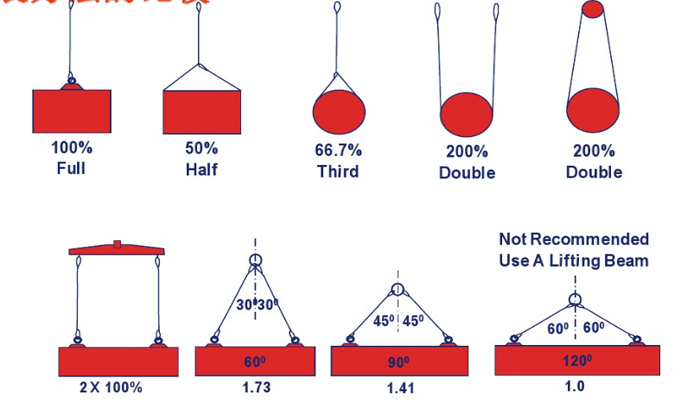
When a wire rope is bent around any sheave or other object there is a loss of strength due to this bending action. As the D/d ratio becomes smaller this loss of strength becomes greater and the rope becomes less efficient. This curve relates the efficiency of a rope diameter to different D/d ratios. This curve is based on static loads and applies to 6-strand class 6×19 and 6×37 wire rope.

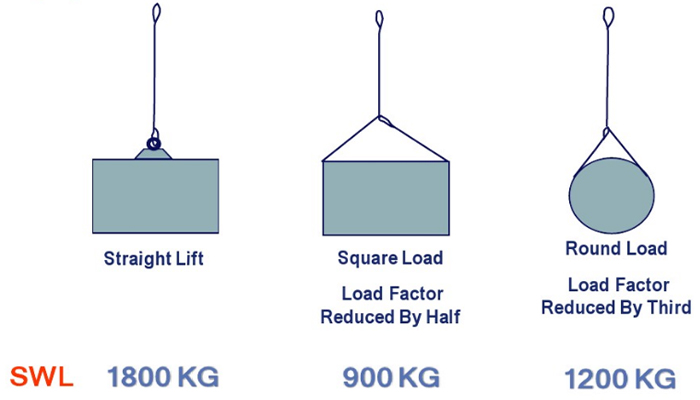
For example: The BASKET and CHOKER hitch capacities listed (in all Standards and Regulations) for 6-strand ropes are based on a minimum D/d ratio of 25:1.

An object you place into a 1" diameter 6-strand wire rope sling using a basket- or choker hitch must have a minimum diameter of 25". If the object is smaller than the listed 25:1 D/d ratio the capacity (or WLL) must be decreased. Table A) illustrates the percentage of decrease to be expected.

If the object lifted with a 6-strand wire rope sling in a basket hitch is at least 25 x larger than the sling diameter (D/d 25:1) the basket capacity need not to be adjusted.

Load Hooks must have sufficient thickness to ensure proper sling D/d ratio, particularly when using slings in an inverted basket hitch; that is the sling BODY is placed into the hook and the sling EYES are facing downwards.

The loss of metallic area is the most important factor affecting the quality of wire ropes. Therefore, it is very important to detect the loss of metallic area values of wire rope defects quickly and accurately. At present, the main flux detection approach is one of the most effective methods, and the detection signal is related directly to the metal cross-sectional area of the wire rope. However, when the defect width is less than a specific value, the existence of the leakage magnetic field means that the amount of the magnetic flux change is not only related to the loss of metallic area of the defect but also has a complex nonlinear relationship with the defect width. The resulting calculation is highly complex and means that the loss of metallic area cannot be determined quickly and quantitatively. This article presents an in-depth study of the theoretical basis of magnetic flux detection, analyzes the problems of the main magnetic flux detection method and their causes, and proposes a method to improve main magnetic flux detection using the axial magnetic flux density. Simulation analysis and experimental results show that the method presented in this article can be used to calculate the loss of metallic area values of defects quickly and accurately without the need for complex calculation processes.