wire rope deflection free sample

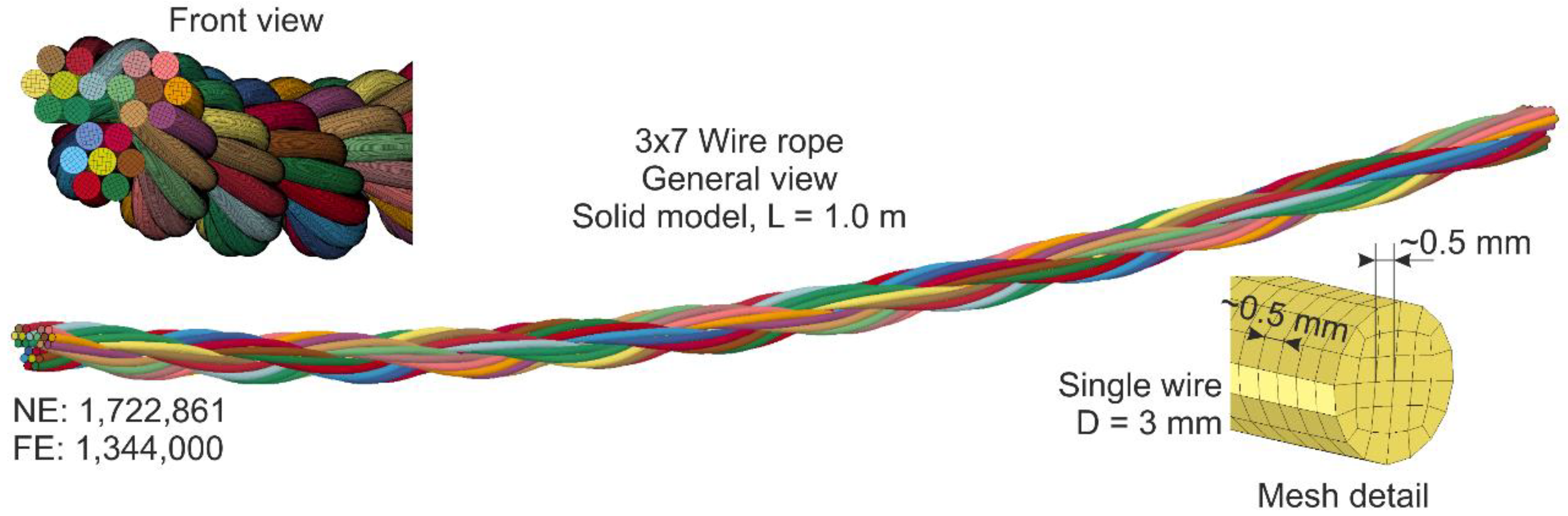
Wire rope is also known by many other names, such as: wire, multi-strand wire, flexible wire, cable, cord, steelcord, etc. but it is essentially a collection of small filaments wound around each other in a manner that largely retains its shape when bent, crushed and/or tensioned.

It is a system for significantly increasing the strength and flexibility of steel wire and is used in almost every important application we see around us. For example: suspension bridges, tyres, brake and accelerator cables (in cars), high-pressure flexible pipes, lifting and rigging cables, electrical conductors, etc. and it comes in many different forms. Fig 2 shows just a very small sample of available designs.

With minor variations, the generally accepted method for designating a wire rope construction in the industry is by describing it numerically. For example:

Whilst "IWRC" wire ropes offer a slightly greater tensile capacity (≈7%) than those with fabric or polymer fillers, the additional strength does not come from the tensile capacity of the core filaments but from improved dimensional stability under load. And whilst they are also much more resistant to crushing, they are stiffer than fibre core ropes and therefore not recommended for applications where tension occurs under bending.

Warrington (Fig 1) is a parallel lay construction with an outer layer comprising wires of alternating large and small diameters, each outer layer having twice the number of wires as the layer immediately beneath. The benefit of this design is to increase packing and therefore strength density, however, unless the different diameter filaments are of the same strength (unlikely), this construction is limited by the strength of the weakest filaments.

Seale (Figs 1 & 2 6x36) is also a parallel lay construction but with the same number of wires in each wire layer. All the wires in any layer are the same diameter. This is an alternative to the Warrington construction, with similar benefits and disadvantages.

Regular lay constructions are used much more widely (than Lang lay) because they have excellent structural stability and less tendency to unwrap under tension (see Rotating vs Non-Rotating below). However, because it has a knobbly (undulating) surface it will wear both itself and any surface over which it is run much more quickly than Lang lay wire rope.

Lang lay constructions have a flatter surface than regular lay constructions giving them better resistance to wear and bending fatigue, especially when made from flattened (elliptical) filaments. They are, however, much less structurally stable and subject to birdcaging if the wire rope is over-bent or twisted against its wrapped direction.

"Regular Lay", multi-strand constructions are normally subject to slightly less rotation under tension (than Lang lay) due to the opposite helical direction of the filaments (within the strands) and the strands (within the rope), however, you can improve their rotation characteristics still further by;

Fillers (Fig 2) may be fabric, polymer or even smaller diameter filaments (e.g. 6x36). Whilst they contribute little to the tensile strength of wire rope, they can significantly; improve performance under bending (fabric and polymer cores only), reduce axial growth, reduce rotation in rotation-resistant constructions, improve structural stability and increase fatigue life.

This filler material should not be included in strength (tensile capacity) calculations, but must be included in those for axial stiffness (extension). If it is ignored, your calculations will reveal excessive extension as the wire rope collapses.

Suspension bridges tend to be constructed from densely packed, single strand plain "Wire Rope" constructions using large diameter galvanised filaments. Little heed is paid to rotational resistance as strength is paramount and once tensioned, they should remain in that loading condition for their design life.

Lifting & winching normally require wire ropes of good flexibility and fatigue resistance. Therefore they tend to be similar to 6x36 but with fibre core instead of the IWRC in Fig 2

Remote operating cables such as hand-brakes and accelerators on cars normally only work in tension so they need to be strong but not necessarily stiff (as they are fully contained in reinforced outer sheaths). These tend to be manufactured from large diameter "TyreCord" or small diameter single-strand "Wire Rope".

Wire rope does not obey Hooke"s law. Therefore, you cannot accurately predict how much it will stretch for any specified force. This unpredictability applies to any section removed from the same manufactured length of cord and even between cords produced to the same specification but by different manufacturers.

CalQlata has decided that the accuracy of axial stiffness (EA) of wire rope falls outside its own levels of acceptability and therefore does not include it in the wire rope calculator. The extension calculated in the Wire Rope calculator (δLᵀ) is based upon the effect of axial tension on packing density. It is therefore important that core material is not ignored when using the calculator to evaluate this characteristic.

Wire rope does not obey Hooke"s law. Therefore, you cannot accurately predict how much it will twist for any specified torque. This unpredictability applies to any section removed from the same manufactured length of cord and even between cords produced to the same specification but by different manufacturers.

CalQlata has decided that the accuracy of torsional stiffness (GJ) of wire rope falls outside its own levels of acceptability and therefore does not include it in the wire rope calculator.

1) No wire rope calculator, whether dedicated or generic, will accurately predict the properties of any single construction under a wide range of loading conditions

2) No wire rope calculator, whether dedicated or generic, will accurately predict any single property for a range of constructions under a wide range of loading conditions

The only wire rope that can be reliably analysed is that which is used for suspension bridges, because; it comprises a single strand, is very densely packed, has negligible twist, contains filaments of only one diameter, is never subjected to minimum bending and every filament is individually tensioned.

There is a very good reason why manufacturers do not present calculated performance data for construction or design proposals, because even they cannot accurately predict such properties and quite rightly rely on, and publish, test data.

During his time working in the industry, the wire rope calculator"s creator has seen, created and abandoned numerous mathematical models both simple and complex. He has gradually developed his own simplified calculation principle based upon his own experience that still provides him with consistently reliable results of reasonable accuracy.

The purpose of CalQlata"s wire rope calculator is to provide its user with the ability to obtain a reasonable approximation for a generic construction, after which, accurate test data should be sought from the manufacturer for the user"s preferred construction.

The calculation principle in the wire rope calculator is based upon changes in the properties of the wire rope that occur with variations in packing density under tension

Bearing in mind the above limitations CalQlata can provide the following assistance when generating (manipulating) the wire rope calculator"s input data and interpreting its output

Alternatively, for wire rope with multiple filament diameters, you need to find an equivalent diameter with the following proviso; you must enter the minimum filament yield stress (SMYS)

It is expected that apart from fillers, all the material in the wire rope will be identical and therefore have the same density, i.e. using different materials will result in less than "best" performance. However, if such a construction is proposed, you can calculate an equivalent density as follows:

It is expected that apart from fillers, all the material in the wire rope will be identical and therefore have the same tensile modulus, i.e. using different materials will result in less than "best" performance. However, if such a construction is proposed, you should enter the highest tensile modulus.

The wire rope calculator simply adds together the total area of all the filaments and multiplies them by the SMYS entered, which represents a theoretical maximum breaking load that would exist if this load is equally shared across all of the filaments and the lay angles have been arranged to eliminate localised (point) loads between adjacent filaments.

If the wire rope has been properly constructed it is likely that its actual break load will be greater than 80% of this theoretical value. However, given the vagaries of wire rope construction, the actual break load can vary considerably dependent upon a number of factors. CalQlata suggest that the following factors may be used to define the anticipated break load of any given construction:

The axial stiffness and strain under load will be affected by this value, hence the reason why the most reliable (predictable) constructions tend to be minimum [number of] strands and single filament diameter. The Warrington and Seale constructions and combinations thereof tend to provide the highest packing density (but lowest flexibility) and there is little to be gained from using these constructions in more than single stranded wire rope as the benefit of high-packing density will be lost with no gain in flexibility.

The anticipated second moment of area of the wire rope at tension "T" due to deformation but insignificant flattening as it is assumed the wire rope will be bent over a formed (shaped) sheave or roller.

The anticipated tensile modulus of the wire rope at tension "T" due to deformation but insignificant flattening as it is assumed the wire rope will be bent over a formed (shaped) sheave or roller.

It is not advisable to induce this bend radius in operation due to uncertainties associated with wire rope construction, especially for dynamic applications. CalQlata suggests that a similar approach to that used for the break load (Fb) above also be applied here, i.e.:

A change in diameter will occur in all wire rope, irrespective of construction, until packing density has reached a limiting value. The value provided in the wire rope calculator is that which would be expected if the construction remains intact at the applied tension "T"

Unreliability of this value increases with complexity in wire rope due to its longitudinal variability and the increased likelihood of premature failure.

The accuracy of this data will range from about ±1% for wire rope with a single strand and a single filament diameter, up to about ±15% for constructions of similar complexity to OTR cord

A change in length of any wire rope will occur due to the fact that the packing density increases with tension. This is not, however, a linear relationship.

This can be an unreliable value as illustrated by tests carried out (by the author) on two pieces of wire rope supplied by the same well-known manufacturer both of which were cut from the same length, varied in tensile capacity by only 1.5%, but the tensile modulus (and strain at break) varied by 34%. Whilst this was an extreme case, significant variations have been seen in wire rope manufactured by a number of manufacturers.

Whilst the wire rope calculator does not calculate axial stiffness (see Calculation Limitations 9) above), CalQlata can suggest the following rule-of-thumb that will provide reasonable results for most constructions at the applied tension "T":

Whilst the wire rope calculator does not calculate bending stiffness (see Calculation Limitations 8) above), CalQlata can suggest the following rule-of-thumb that will provide reasonable results for most constructions at the applied tension "T":

Low complexity means single strand and single wire diameter. Medium complexity means multi-strand and single wire diameter. High complexity means multi-strand and multiple wire diameters.

Wire rope forms an important part of many machines and structures. It is comprised of continuous wire strands wound around a central core. There are many kinds of wire rope designed for different applications. Most of them are steel wires made into strands wound with each other. The core can be made of steel, rope or even plastics.

Wire ropes (cables) are identified by several parameters including size, grade of steel used, whether or not it is preformed, by its lay, the number of strands and the number of wires in each strand.

A typical strand and wire designation is 6x19. This denotes a rope made up of six strands with 19 wires in each strand. Different strand sizes and arrangements allow for varying degrees of rope flexibility and resistance to crushing and abrasion. Small wires are better suited to being bent sharply over small sheaves (pulleys). Large outer wires are preferred when the cable will be rubbed or dragged through abrasives.

There are three types of cores. An independent wire rope core (IWRC) is normally a 6x7 wire rope with a 1x7 wire strand core resulting in a 7x7 wire rope. IWRCs have a higher tensile and bending breaking strength than a fiber core rope and a high resistance to crushing and deformation.

A wire strand core (WSC) rope has a single wire strand as its core instead of a multistrand wire rope core. WSC ropes are high strength and are mostly used as static or standing ropes.

Wire ropes also have fiber cores. Fiber core ropes were traditionally made with sisal rope, but may also use plastic materials. The fiber core ropes have less strength than steel core ropes. Fiber core ropes are quite flexible and are used in many overhead crane applications.

The lay of a wire rope is the direction that the wire strands and the strands in the cable twist. There are four common lays: right lay, left lay, regular lay and lang lay. In a right lay rope the strands twist to the right as it winds away from the observer. A left lay twists to the left. A regular lay rope has the wires in the strands twisted in the opposite direction from the strands of the cable. In a lang lay rope, the twist of the strands and the wires in the strands are both twisted the same way. Lang lay ropes are said to have better fatigue resistance due to the flatter exposure of the wires.

Wire ropes are made mostly from high carbon steel for strength, versatility, resilience and availability and for cost consideration. Wire ropes can be uncoated or galvanized. Several grades of steel are used and are described in Table 1.

Steel cable wire is stiff and springy. In nonpreformed rope construction, broken or cut wires will straighten and stick out of the rope as a burr, posing a safety hazard. A preformed cable is made of wires that are shaped so that they lie naturally in their position in the strand, preventing the wires from protruding and potentially causing injury. Preformed wire ropes also have better fatigue resistance than nonpreformed ropes and are ideal for working over small sheaves and around sharp angles.

Lubricating wire ropes is a difficult proposition, regardless of the construction and composition. Ropes with fiber cores are somewhat easier to lubricate than those made exclusively from steel materials. For this reason, it is important to carefully consider the issue of field relubrication when selecting rope for an application.

There are two types of wire rope lubricants, penetrating and coating. Penetrating lubricants contain a petroleum solvent that carries the lubricant into the core of the wire rope then evaporates, leaving behind a heavy lubricating film to protect and lubricate each strand (Figure 2). Coating lubricants penetrate slightly, sealing the outside of the cable from moisture and reducing wear and fretting corrosion from contact with external bodies.

Both types of wire rope lubricants are used. But because most wire ropes fail from the inside, it is important to make sure that the center core receives sufficient lubricant. A combination approach in which a penetrating lubricant is used to saturate the core, followed with a coating to seal and protect the outer surface, is recommended. Wire rope lubricants can be petrolatum, asphaltic, grease, petroleum oils or vegetable oil-based (Figure 3).

Petrolatum compounds, with the proper additives, provide excellent corrosion and water resistance. In addition, petrolatum compounds are translucent, allowing the technician to perform visible inspection. Petrolatum lubricants can drip off at higher temperatures but maintain their consistency well under cold temperature conditions.

Various types of greases are used for wire rope lubrication. These are the coating types that penetrate partially but usually do not saturate the rope core. Common grease thickeners include sodium, lithium, lithium complex and aluminum complex soaps. Greases used for this application generally have a soft semifluid consistency. They coat and achieve partial penetration if applied with pressure lubricators.

Petroleum and vegetable oils penetrate best and are the easiest to apply because proper additive design of these penetrating types gives them excellent wear and corrosion resistance. The fluid property of oil type lubricants helps to wash the rope to remove abrasive external contaminants.

Wire ropes are lubricated during the manufacturing process. If the rope has a fiber core center, the fiber will be lubricated with a mineral oil or petrolatum type lubricant. The core will absorb the lubricant and function as a reservoir for prolonged lubrication while in service.

If the rope has a steel core, the lubricant (both oil and grease type) is pumped in a stream just ahead of the die that twists the wires into a strand. This allows complete coverage of all wires.

After the cable is put into service, relubrication is required due to loss of the original lubricant from loading, bending and stretching of the cable. The fiber core cables dry out over time due to heat from evaporation, and often absorb moisture. Field relubrication is necessary to minimize corrosion, protect and preserve the rope core and wires, and thus extend the service life of the wire rope.

If a cable is dirty or has accumulated layers of hardened lubricant or other contaminants, it must be cleaned with a wire brush and petroleum solvent, compressed air or steam cleaner before relubrication. The wire rope must then be dried and lubricated immediately to prevent rusting. Field lubricants can be applied by spray, brush, dip, drip or pressure boot. Lubricants are best applied at a drum or sheave where the rope strands have a tendency to separate slightly due to bending to facilitate maximum penetration to the core. If a pressure boot application is used, the lubricant is applied to the rope under slight tension in a straight condition. Excessive lubricant application should be avoided to prevent safety hazards.

Some key performance attributes to look for in a wire rope lubricant are wear resistance and corrosion prevention. Some useful performance benchmarks include high four-ball EP test values, such as a weld point (ASTM D2783) of above 350 kg and a load wear index of above 50. For corrosion protection, look for wire rope lubricants with salt spray (ASTM B117) resistance values above 60 hours and humidity cabinet (ASTM D1748) values of more than 60 days. Most manufacturers provide this type of data on product data sheets.

Cable life cycle and performance are influenced by several factors, including type of operation, care and environment. Cables can be damaged by worn sheaves, improper winding and splicing practices, and improper storage. High stress loading, shock loading, jerking heavy loads or rapid acceleration or deceleration (speed of the cable stopping and starting) will accelerate the wear rate.

Corrosion can cause shortened rope life due to metal loss, pitting and stress risers from pitting. If a machine is to be shut down for an extended period, the cables should be removed, cleaned, lubricated and properly stored. In service, corrosion and oxidation are caused by fumes, acids, salt brines, sulfur, gases, salt air, humidity and are accelerated by elevated temperatures. Proper and adequate lubricant application in the field can reduce corrosive attack of the cable.

Abrasive wear occurs on the inside and outside of wire ropes. Individual strands inside the rope move and rub against one another during normal operation, creating internal two-body abrasive wear. The outside of the cable accumulates dirt and contaminants from sheaves and drums. This causes three-body abrasive wear, which erodes the outer wires and strands. Abrasive wear usually reduces rope diameter and can result in core failure and internal wire breakage. Penetrating wire rope lubricants reduce abrasive wear inside the rope and also wash off the external surfaces to remove contaminants and dirt.

Many types of machines and structures use wire ropes, including draglines, cranes, elevators, shovels, drilling rigs, suspension bridges and cable-stayed towers. Each application has specific needs for the type and size of wire rope required. All wire ropes, regardless of the application, will perform at a higher level, last longer and provide greater user benefits when properly maintained.

Lubrication Engineers, Inc. has found through years of field experience, that longer wire rope life can be obtained through the use of penetrating lubricants, either alone or when used in conjunction with a coating lubricant. Practical experience at a South African mine suggests that life cycles may be doubled with this approach. At one mine site, the replacement rate for four 44-mm ropes was extended from an average 18.5 months to 43 months. At another mine, life cycles of four 43-mm x 2073 meter ropes were extended from an average 8 months to 12 months.

In another study involving 5-ton and 10-ton overhead cranes in the United States that used 3/8-inch and 5/8-inch diameter ropes, the average life of the ropes was doubled. The authors attribute this increased performance to the ability of the penetrating lubricant to displace water and contaminants while replacing them with oil, which reduces the wear and corrosion occurring throughout the rope. A good spray with penetrating wire rope lubricant effectively acts as an oil change for wire ropes.

In these examples, the savings in wire rope replacement costs (downtime, labor and capital costs) were substantial and dwarfed the cost of the lubricants. Companies who have realized the importance of proper wire rope lubrication have gained a huge advantage over those who purchase the lowest priced lubricant, or no lubricant at all, while replacing ropes on a much more frequent basis.

Check-Line cable tension meters are designed for a wide range of applications include measuring tension of guy wires, wire rope, tower rigging, over head lines and more. We offer cable tension meters for fixed spans and running lines. Please contact us to review your application and help you select the best model for your requirements.

New here? Try reading these, they might help FAQ731-376: Eng-Tips.com Forum Policies http://eng-tips.com/market.cfm? RE: Increased tension in wire rope

New here? Try reading these, they might help FAQ731-376: Eng-Tips.com Forum Policies http://eng-tips.com/market.cfm? RE: Increased tension in wire rope

Handleman... if I understand the problem, it"s not so trivial...it"s deceptive. The cable has an initial load of 100 Kg and an initial sag; there is no reference to the cable weight or material (assumed to be steel and fy and Es not known) and a length of 6.5 m. The 8.5 Kg load applied to the center causes it to deflect 150mm. I"m not sure how that is arrived at, by measurement? In a pinch, you can establish the dia of the cable from the above info, but, it"s very complicated. With a horizontal (nearly) cable, any load applied at mid span increases the tension substantially and as it deflects this tension is relieved a bit. If at the end of the day, the total deflection is 150 mm it is a difficult solution. It could be that the weight of the cable approaches, or exceeds the weight in the middle and the weight of the cable cannot be eliminated. Definitely not a simple question problem.

OP already stated that the measured deflection due to sag is 2mm. Compared with the 150mm measured deflection under 8.5KGF load, the sag is negligible.

Again, this is statics. It is true. Therefore, something is incorrect with the OP"s setup. Let"s examine the likely culprits. 6.5mm span? Not so likely. Easy to measure. Same with deflection amount and actual mass of applied weight. That leaves tension. OP has already stated that tensometer accuracy is questionable, because the measured increase was "5-10kgf". Therefore, the obvious conclusion is that the initial 100kgf measurement is inaccurate.

The OP specifically stated point load at the center. This is most certainly NOT a catenary. Catenary is the shape created by the distributed weight load of a hanging rope/chain due to its own weight. OP specifically stated that the measured sag (which is a catenary) before weight was added is 2mm. A 2mm catenary over 6.5m. This is pretty negligible for our purposes, as compared with the 150mm deflection induced by the weight.

But, just for fun, we can find the approximate weight of the 6.5m rope if it makes us feel any better. We"re already doubting the initial tension statement, but, giving a window of 90 to 110kgf actual tension, our window for total mass of the 6.5m rope is somewhere between 0.23kg and 0.28kg. (verification left as an exercise) Again, insignificant compared to the 8.5kg weight hanging from the center.

So, given that we know the final tension, how can we find the initial tension? Again, as rb mentioned, it has everything to do with the strain of the rope.

Let"s consider what we know to be true: 8.5kg weight hanging at 150mm deflection from a 6.5m span. Now, imagine 2 different ropes. First, consider a theoretically perfectly zero stretch rope. What happens when you remove the weight? What is the tension? Almost nothing. It will fall into a loose catenary with the same length as the 2 hypotenii. Interestingly enough, since we already calculated the weight of the actual rope is apx 0.25kgf, we can calculate the catenary sag amount as apx 130mm, and the cable tension somewhere around 1.6 kgf for this completely non-stretch rope (another exercise for the reader). Now let"s consider a rubber band. It"s a really long rubber band. and it has a "spring constant", if you will, of 1kgf/mm. When you remove the center weight, the band contracts and goes horizontal (ignoring its mass). We can easily calculate the length difference between the hypotenii and the horizontal as apx. 7mm. Since the spring constant is 1kgf/mm, the pre-weight tension is calculated to be 92kgf-7kgf=85kgf. What if the rubber band is a bit stretchier? Like 0.1kgf/mm? Then the initial tension would be only 92-70=22kgf.

Of course, as I mentioned earlier this all assumes perfect rigidity from the entire system, such that all of the geometry change between the 2mm catenary and the 150mm deflection is due to stretch of the rope. If your stand or anchors are deflecting, or the tensometer somehow has a not-insignificant spring rate, all bets are off.

The tensiometer probably has a lot of inherent error in it that can"t give a reliable reading with the initial tension and added tension, it provides some solid confusion. Much better would be a spring scale on one end. RE: Increased tension in wire rope

I think that the OP was badly stated "The wire rope is 6.5m in length and prestressed to 100Kgs a load of 8.5kgs is applied to the center...." There should have been a period after the 100Kgs then a different picture presents itself as "The wire rope is 6.5m in length and prestressed to 100Kgs. A load of 8.5kgs is applied to the center..." . The 100 kgs prestress is to stretch the rope only. Afterward the 8 kgs is applied in a cable that is inextensible. The cable, first is under gravity acting as a catenary and secondly under the point load of 8Kgs which can be solved by vectors as pointed above. The catenary evalustion may not be necessary depending of the unit weight of the cable. For a reference into solving this type of problem, here is the title and author as I don"t have the link "; I don"t have the link but here is the thesis and its author "ON SHAPE CONTROL OF CABLES UNDER VERTICAL STATIC LOADS-DANIEL PAPINI". Page 61 is the reference needed. RE: Increased tension in wire rope

Ash. On my web site (http://rmniall.com) you will find a free downloadable spreadsheet that gives a rigorous analysis for the problem of a (single) point load applied to a cable. The cable can be inclined from horizontal, the load can be inclined from vertical, and the cable can be extensible. RE: Increased tension in wire rope

While simple statics reasonably gives 92 kg tension in the rope, a basic assumption of this is that the angle of the rope at the point load is defined by the rise and the run, and neglects any curvature of the rope, which we know exists.

Taking the angle as asin (W/2T) and T as 105kgf, I get 2.3*, which is a hair less than the 2.5* stated above. I"m happy with that. RE: Increased tension in wire rope

Moon161. "No dice"? I"m always looking for ways to improve my spreadsheets, so if you can tell me what particular dice my cable spreadsheet lacks I might be able to accommodate whatever it is you are looking for. Contact via the e-mail address in the spreadsheet and on my web site would be best. RE: Increased tension in wire rope

This is similar (equi-anglular) to the displacement triangle so displacement = 4.25/110 x 3250 = 125.6 mm. This is slightly less than the measured displacement (150mm) because the rope has some bending stiffness and the centre section of the rope acts like a beam.

Most errors with the spreadsheet went away when I extracted the .xls from the zip to a folder instead of opening from the .zip file. RE: Increased tension in wire rope

Do you need to use trig tables and introduce rounding errors? Also not sure why you have used tan and asin for similar triangles. Again I guess you are assuming the supports are rigid and the cable has stretched? I am still surprised there is 5% difference in our deflection result (126 vs 132mm).

But the only way I can get the geometry to work (150 mm deflection at center after a 8.5 Kg weight is applied at the center) is if the tension is applied by a 200 Kg weight pulling the wire rope (cable) over a pulley. The minute extra expansion of the stretch of the cable cannot the whole length long enough to create that 2.64 degree angle from the straight case. The total wire length between two points 6500 mm long with a 150 mm vertical is 6506.9 mm. You"d be claiming the cable stretched 7 mm.

Now, the "cable" might stretch that much by the slipping and "unkinking" of the individual wire strands against each other, but the "metal" itself would not stretch that much if it were a solid cylinder of uniform cross-section.

And the orignal 200 Kg weight should remove much of that "mechanical" wire fiber unkinking and slip from the initial "unstressed" condition to its t=0 straight length before putting the 8.5 Kg weight on. RE: Increased tension in wire rope

You"d be claiming the cable stretched 7 mm. Now, the "cable" might stretch that much by the slipping and "unkinking" of the individual wire strands against each other, but the "metal" itself would not stretch that much if it were a solid cylinder of uniform cross-section.

Why not? The cable is small. As handleman points out, the total mass of the 6.5m rope is only ~.25kg. My quick calculation shows that 7mm is plausible.