mud pump calculations free sample

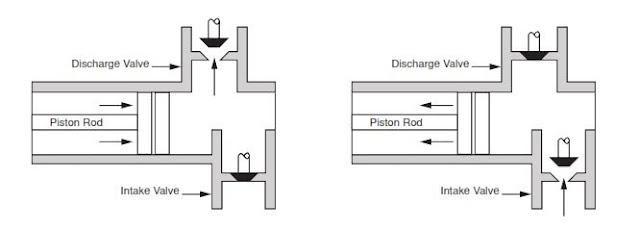
Rig pump output, normally in volume per stroke, of mud pumps on the rig is  one of important figures that we really need to know because we will use pump out put figures to calculate many parameters such as bottom up strokes,  wash out depth, tracking drilling fluid, etc. In this post, you will learn how to calculate pump out put for triplex pump and duplex pump in bothOilfield and Metric Unit.

Oil and Gas drilling process - Pupm output for Triplex and Duplex pumpsTriplex Pump Formula 1 PO, bbl/stk = 0.000243 x ( in) E.xample: Determine the pump output, bbl/stk, at 100% efficiency for a 7" by 12". triplex pump: PO @ 100%,= 0.000243 x 7 x12 PO @ 100% = 0.142884bbl/stk Adjust the pump output for 95% efficiency: Decimal equivalent = 95 + 100 = 0.95 PO @ 95% = 0.142884bbl/stk x 0.95 PO @ 95% = 0.13574bbl/stk Formula 2 PO, gpm = [3(D x 0.7854)S]0.00411 x SPM where D = liner diameter, in. S = stroke length, in. SPM = strokes per minute Determine the pump output, gpm, for a 7" by 12". triplex pump at 80 strokes per minute: PO, gpm = [3(7 x 0.7854) 1210.00411 x 80 PO, gpm = 1385.4456 x 0.00411 x 80 PO = 455.5 gpm

Example:Duplex Pump Formula 1 0.000324 x (liner diameter, in) x ( stroke lengh, in) = ________ bbl/stk -0.000162 x (rod diameter, in) x ( stroke lengh, in) = ________ bbl/stk Pump out put @ 100% eff = ________bbl/stk Example: Determine the output, bbl/stk, of a 5 1/2" by 14" duplex pump at 100% efficiency. Rod diameter = 2.0": 0.000324 x 5.5 x 14 = 0.137214bbl/stk -0.000162 x 2.0 x 14 = 0.009072bbl/stk Pump output @ 100% eff. = 0.128142bbl/stk Adjust pump output for 85% efficiency: Decimal equivalent = 85 100 = 0.85 PO@85%)= 0.128142bbl/stk x 0.85 PO@ 85% = 0.10892bbl/stk Formula 2

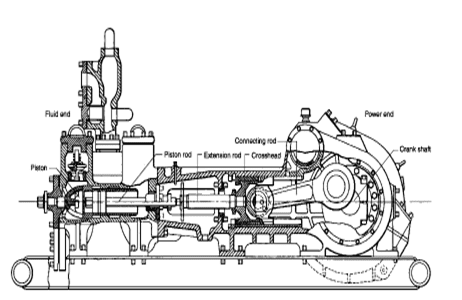
PO. bbl/stk = 0.000162 x S[2(D) - d] where S = stroke length, in. D = liner diameter, in. d = rod diameter, in. Example: Determine the output, bbl/stk, of a 5 1/2". by 14". duplex pump @ 100% efficiency. Rod diameter = 2.0in.: PO@100%=0.000162 x 14 x [ 2 (5.5) - 2 ] PO @ 100%)= 0.000162 x 14 x 56.5 PO@ 100%)= 0.128142bbl/stk Adjust pump output for 85% efficiency: PO@85%,= 0.128142bb/stkx 0.85 PO@8.5%= 0.10892bbl/stk Metric calculation Pump output, liter/min = pump output. liter/stk x pump speed, spm. S.I. units calculation Pump output, m/min = pump output, liter/stk x pump speed, spm. Mud Pumps Mud pumps drive the mud around the drilling system. Depending on liner size availability they can be set up to provide high pressure and low flow rate, or low pressure and high flow rate. Analysis of the application and running the Drill Bits hydraulics program will indicate which liners to recommend. Finding the specification of the mud pumps allows flow rate to be calculated from pump stroke rate, SPM. Information requiredo Pump manufacturer o Number of pumps o Liner size and gallons per revolution Weight As a drill bit cutting structure wears more weight will be required to achieve the same RoP in a homogenous formation. PDC wear flats, worn inserts and worn milled tooth teeth will make the bit drill less efficiently. Increase weight in increments of 2,000lbs approx. In general, weight should be applied before excessive rotary speed so that the cutting structure maintains a significant depth of cut to stabilise the bit and prevent whirl. If downhole weight measurements are available they can be used in combination with surface measurements to gain a more accurate representation of what is happening in the well bore.

Pumps tend to be one of the biggest energy consumers in industrial operations. Pump motors, specifically, require a lot of energy. For instance, a 2500 HP triplex pump used for frac jobs can consume almost 2000 kW of power, meaning a full day of fracking can cost several thousand dollars in energy costs alone!

So, naturally, operators should want to maximize energy efficiency to get the most for their money. Even a 1% improvement in efficiency can decrease annual pumping costs by tens of thousands of dollars. The payoff is worth the effort. And if you want to remotely control your pumps, you want to keep efficiency in mind.

In this post, we’ll point you in the right direction and discuss all things related to pump efficiency. We’ll conclude with several tips for how you can maintain pumping efficiency and keep your energy costs down as much as possible.

In simple terms, pump efficiency refers to the ratio of power out to power in. It’s the mechanical power input at the pump shaft, measured in horsepower (HP), compared to the hydraulic power of the liquid output, also measured in HP. For instance, if a pump requires 1000 HP to operate and produces 800 HP of hydraulic power, it would have an efficiency of 80%.

Remember: pumps have to be driven by something, i.e., an electric or diesel motor. True pump system efficiency needs to factor in the efficiency of both the motor AND the pump.

Consequently, we need to think about how electrical power (when using electric motors) or heat power (when using combustion engines) converts into liquid power to really understand pump efficiency.

Good pump efficiency depends, of course, on pump type and size. High-quality pumps that are well-maintained can achieve efficiencies of 90% or higher, while smaller pumps tend to be less efficient. In general, if you take good care of your pumps, you should be able to achieve 70-90% pump efficiency.

Now that we have a better understanding of the pump efficiency metric, let’s talk about how to calculate it. The mechanical power of the pump, or the input power, is a property of the pump itself and will be documented during the pump setup. The output power, or hydraulic power, is calculated as the liquid flow rate multiplied by the "total head" of the system.

IMPORTANT: to calculate true head, you also need to factor in the work the pump does to move fluid from the source. For example, if the source water is below the pump, you need to account for the extra work the pump puts in to draw source water upwards.

*Note - this calculation assumes the pump inlet is not pressurized and that friction losses are minimal. If the pump experiences a non-zero suction pressure, or if there is significant friction caused by the distance or material of the pipe, these should be factored in as well.

You"ll notice that the elevation head is minimal compared to the discharge pressure, and has minimal effect on the efficiency of the pump. As the elevation change increases or the discharge pressure decreases, however, elevation change will have a greater impact on total head.

Obviously, that’s a fair amount of math to get at the pump efficiency, considering all of the units conversions that need to be done. To avoid doing these calculations manually, feel free to use our simple pump efficiency calculator.

Our calculations use static variables (pump-rated horsepower and water source elevation) and dynamic variables (discharge flow and pressure). To determine pump efficiency, we need to measure the static variables only once, unless they change.

If you want to measure the true efficiency of your pump, taking energy consumption into account, you could add an electrical meter. Your meter should consist of a current transducer and voltage monitor (if using DC) for electrical motors or a fuel gauge for combustion. This would give you a true understanding of how pump efficiency affects energy consumption, and ultimately your bank account.

Up until this point, we’ve covered the ins and outs of how to determine pump efficiency. We’re now ready for the exciting stuff - how to improve pump efficiency!

One of the easiest ways to improve pump efficiency is to actually monitor pumps for signs of efficiency loss! If you monitor flow rate and discharge (output power) along with motor current or fuel consumption, you’ll notice efficiency losses as soon as they occur. Simply having pump efficiency information on hand empowers you to take action.

Another way to increase efficiency is to keep pumps well-maintained. Efficiency losses mostly come from mechanical defects in pumps, e.g., friction, leakages, and component failures. You can mitigate these issues through regular maintenance that keeps parts in working order and reveals impending failures. Of course, if you are continuously monitoring your pumps for efficiency drops, you’ll know exactly when maintenance is due.

You can also improve pump efficiency by keeping pumps lubricated at all times. Lubrication is the enemy of friction, which is the enemy of efficiency (“the enemy of my enemy is my friend…”).

A fourth way to enhance pump efficiency is to ensure your pumps and piping are sized properly for your infrastructure. Although we’re bringing this up last, it’s really the first step in any pumping operation. If your pumps and piping don’t match, no amount of lubricant or maintenance will help.

In this post, we’ve given you the full rundown when it comes to calculating and improving pump efficiency. You can now calculate, measure, and improve pump efficiency, potentially saving your business thousands of dollars annually on energy costs.

For those just getting started with pump optimization, we offer purpose-built, prepackaged solutions that will have you monitoring pump efficiency in minutes, even in hazardous environments.

Tri-Axial Casing Design is a completely new version of casing design covering both Bi-Axial and Tri-Axial calculations for bending, collapse and tension stress changes based in the maximum dog leg severity between Well Head and Casing Shoe. Including the option to look up the maximum DLS between any selected depths MD 1 to MD 2. The program picks the maximum DLS between the user inputs.

API rated burst strength is de-rated for temperatures from 10 to 600 F° (-12 to 316 C°) Drilling Condition – Gas/oil kick while drilling below the shoe with partial or total mud evacuation (user selects evac percent), with shut in pressurized column of gas/oil to surface and old mud weight gradient behind casing. The old MW that was behind the casing when it was cemented is used for annulus hydrostatic burst calculations and the present MW is used for internal hydrostatic calculations. The user inputs the gas/oil gradient that most closely fits their design for internal pressure gradient.

Production burst loads are calculated assuming a full shut in column of pressured gas/oil (i.e. 100% mud evacuation), with Leakoff EMW pressure at the shoe and a column of salt water behind the casing. .

Drilling collapse loads are calculated assuming the casing has been partially or fully evacuated of mud (resulting from lost circulation, or a blowout), while drilling below the shoe, with a non-pressured column of gas/oil to the surface (i.e. atmospheric pressure at the surface) and a full column of old MW behind the casing. The user inputs the gas/oil gradient that most closely fits their design for internal pressure gradient.

. Production collapse loads are calculated assuming 100% mud evacuation with an un-pressured column of gas/oil to the surface. The old MW that was behind the casing when it was cemented is used for annulus hydrostatic collapse calculations. The user inputs the gas/oil gradient that most closely fits their design for internal pressure gradient.

Cementing Collapse loads are calculated with applicable hydrostatic columns of mud and cement slurries outside the casing and displacement fluid column inside the casing. The small hydrostatic difference of the cement in the shoe joints is ignored and displacement fluid is assumed to the shoe TVD. Cementing collapse is typically a concern with big OD conductors and surface casings.

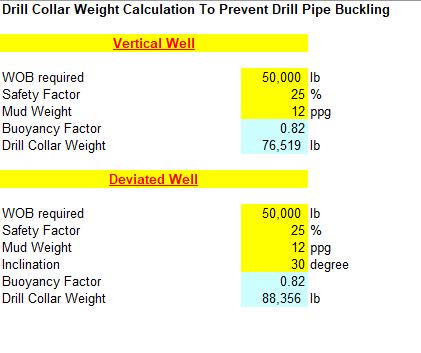
Tensile analysis considers the total hanging weight of the casing as it is being run in the hole. The user selects Vertical or Directional tensile analysis to calculate tensile loads assuming buoyant weight of steel in a mud filled hole. . Buoyancy factor = (65.4-MW)/65.4

Tri-Axial Casing Design includes a combination of csg and Liner installation, the new version of Casing Design now includes liner overlap calculations

When two (or more) pumps are arranged in serial their resulting pump performance curve is obtained by adding theirheads at the same flow rate as indicated in the figure below.

Centrifugal pumps in series are used to overcome larger system head loss than one pump can handle alone. for two identical pumps in series the head will be twice the head of a single pump at the same flow rate - as indicated with point 2.

With a constant flowrate the combined head moves from 1 to 2 - BUTin practice the combined head and flow rate moves along the system curve to point 3. point 3 is where the system operates with both pumps running

When two or more pumps are arranged in parallel their resulting performance curve is obtained by adding the pumps flow rates at the same head as indicated in the figure below.

Centrifugal pumps in parallel are used to overcome larger volume flows than one pump can handle alone. for two identical pumps in parallel and the head kept constant - the flow rate doubles compared to a single pump as indicated with point 2

Note! In practice the combined head and volume flow moves along the system curve as indicated from 1 to 3. point 3 is where the system operates with both pumps running

In practice, if one of the pumps in parallel or series stops, the operation point moves along the system resistance curve from point 3 to point 1 - the head and flow rate are decreased.

A kick is a well control problem in which the pressure found within the drilled rock is higher than the mud hydrostatic pressure acting on the borehole or rock face. When this occurs, the greater formation pressure has a tendency to force formation fluids into the wellbore. This forced fluid flow is called a kick. If the flow is successfully controlled, the kick is considered to have been killed. An uncontrolled kick that increases in severity may result in what is known as a “blowout.”

Yet another factor affecting kick severity is the “pressure differential” involved. Pressure differential is the difference between the formation fluid pressure and the mud hydrostatic pressure. If the formation pressure is much greater than the hydrostatic pressure, a large negative differential pressure exists. If this negative differential pressure is coupled with high permeability and high porosity, a severe kick may occur.

Another way of labeling kicks is by identifying the required mud weight increase necessary to control the well and kill a potential blowout. For example, if a kick required a 0.7-lbm/gal (84-kg/m3) mud weight increase to control the well, the kick could be termed a 0.7-lbm/gal (84-kg/m3) kick. It is interesting to note that an average kick requires approximately 0.5 lbm/gal (60 kg/m3), or less, mud weight increase.

Kicks occur as a result of formation pressure being greater than mud hydrostatic pressure, which causes fluids to flow from the formation into the wellbore. In almost all drilling operations, the operator attempts to maintain a hydrostatic pressure greater than formation pressure and, thus, prevent kicks; however, on occasion the formation will exceed the mud pressure and a kick will occur. Reasons for this imbalance explain the key causes of kicks:

Insufficient mud weight is the predominant cause of kicks. A permeable zone is drilled while using a mud weight that exerts less pressure than the formation pressure within the zone. Because the formation pressure exceeds the wellbore pressure, fluids begin to flow from the formation into the wellbore and the kick occurs.

These abnormal formation pressures are often associated with causes for kicks. Abnormal formation pressures are greater pressures than in normal conditions. In well control situations, formation pressures greater than normal are the biggest concern. Because a normal formation pressure is equal to a full column of native water, abnormally pressured formations exert more pressure than a full water column. If abnormally pressured formations are encountered while drilling with mud weights insufficient to control the zone, a potential kick situation has developed. Whether or not the kick occurs depends on the permeability and porosity of the rock. A number of abnormal pressure indicators can be used to estimate formation pressures so that kicks caused by insufficient mud weight are prevented (some are listed in Table 1).

An obvious solution to kicks caused by insufficient mud weights seems to be drilling with high mud weights; however, this is not always a viable solution. First, high mud weights may exceed the fracture mud weight of the formation and induce lost circulation. Second, mud weights in excess of the formation pressure may significantly reduce the penetration rates. Also, pipe sticking becomes a serious consideration when excessive mud weights are used. The best solution is to maintain a mud weight slightly greater than formation pressure until the mud weight begins to approach the fracture mud weight and, thus, requires an additional string of casing.

Improperly filling up of the hole during trips is another prominent cause of kicks. As the drillpipe is pulled out of the hole, the mud level falls because the pipe steel no longer displaces the mud. As the overall mud level decreases, the hole must be periodically filled up with mud to avoid reducing the hydrostatic pressure and, thereby, allowing a kick to occur.

Several methods can be used to fill up the hole, but each must be able to accurately measure the amount of mud required. It is not acceptable—under any condition—to allow a centrifugal pump to continuously fill up the hole from the suction pit because accurate mud-volume measurement with this sort of pump is impossible. The two acceptable methods most commonly used to maintain hole fill-up are the trip-tank method and the pump-stroke measurements method.

The trip-tank method has a calibration device that monitors the volume of mud entering the hole. The tank can be placed above the preventer to allow gravity to force mud into the annulus, or a centrifugal pump may pump mud into the annulus with the overflow returning to the trip tank. The advantages of the trip-tank method include that the hole remains full at all times, and an accurate measurement of the mud entering the hole is possible.

The other method of keeping a full hole—the pump-stroke measurement method—is to periodically fill up the hole with a positive-displacement pump. A flowline device can be installed with the positive-displacement pump to measure the pump strokes required to fill the hole. This device will automatically shut off the pump when the hole is full.

Gas-contaminated mud will occasionally cause a kick, although this is rare. The mud density reduction is usually caused by fluids from the core volume being cut and released into the mud system. As the gas is circulated to the surface, it expands and may reduce the overall hydrostatic pressure sufficient enough to allow a kick to occur.

Although the mud weight is cut severely at the surface, the hydrostatic pressure is not reduced significantly because most gas expansion occurs near the surface and not at the hole bottom.

Occasionally, kicks are caused by lost circulation. A decreased hydrostatic pressure occurs from a shorter mud column. When a kick occurs from lost circulation, the problem may become severe. A large volume of kick fluid may enter the hole before the rising mud level is observed at the surface. It is recommended that the hole be filled with some type of fluid to monitor fluid levels if lost circulation occurs.

An increase in flow rate leaving the well, while pumping at a constant rate, is a primary kick indicator. The increased flow rate is interpreted as the formation aiding the rig pumps by moving fluid up the annulus and forcing formation fluids into the wellbore.

If the pit volume is not changed as a result of surface-controlled actions, an increase indicates a kick is occurring. Fluids entering the wellbore displace an equal volume of mud at the flowline, resulting in pit gain.

When the rig pumps are not moving the mud, a continued flow from the well indicates a kick is in progress. An exception is when the mud in the drillpipe is considerably heavier than in the annulus, such as in the case of a slug.

A pump pressure change may indicate a kick. Initial fluid entry into the borehole may cause the mud to flocculate and temporarily increase the pump pressure. As the flow continues, the low-density influx will displace heavier drilling fluids, and the pump pressure may begin to decrease. As the fluid in the annulus becomes less dense, the mud in the drillpipe tends to fall and pump speed may increase.

Other drilling problems may also exhibit these signs. A hole in the pipe, called a “washout,” will cause pump pressure to decrease. A twist-off of the drillstring will give the same signs. It is proper procedure, however, to check for a kick if these signs are observed.

When the drillstring is pulled out of the hole, the mud level should decrease by a volume equivalent to the removed steel. If the hole does not require the calculated volume of mud to bring the mud level back to the surface, it is assumed a kick fluid has entered the hole and partially filled the displacement volume of the drillstring. Even though gas or salt water may have entered the hole, the well may not flow until enough fluid has entered to reduce the hydrostatic pressure below the formation pressure.

Drilling fluid provides a buoyant effect to the drillstring and reduces the actual pipe weight supported by the derrick. Heavier muds have a greater buoyant force than less dense muds. When a kick occurs, and low-density formation fluids begin to enter the borehole, the buoyant force of the mud system is reduced, and the string weight observed at the surface begins to increase.

Fortunately, the lower mud weights from the cuttings effect are found near the surface (generally because of gas expansion), and do not appreciably reduce mud density throughout the hole. Table 3 shows that gas cutting has a very small effect on bottomhole hydrostatic pressure.

An important point to remember about gas cutting is that, if the well did not kick within the time required to drill the gas zone and circulate the gas to the surface, only a small possibility exists that it will kick. Generally, gas cutting indicates that a formation has been drilled that contains gas. It does not mean that the mud weight must be increased.

The MWD tool enables monitoring of the acoustic properties of the annulus for early gas-influx detection. Pressure pulses generated by the MWD pulser are recorded and compared at the standpipe and the top of the annulus. Full-scale testing has shown that the presence of free gas in the annulus is detected by amplitude attenuation and phase delay between the two signals. For water-based mud systems, this technique has demonstrated the capacity to consistently detect gas influxes within minutes before significant expansion occurs. Further development is currently under way to improve the system’s capability to detect gas influxes in oil-based mud.

Some MWD tools feature kick detection through ultrasonic sensors. In these systems, an ultrasonic transducer emits a signal that is reflected off the formation and back to the sensor. Small quantities of free gas significantly alter the acoustic impedance of the mud. Automatic monitoring of these signals permits detection of gas in the annulus. It should be noted that these devices only detect the presence of gas at or below the MWD tool.

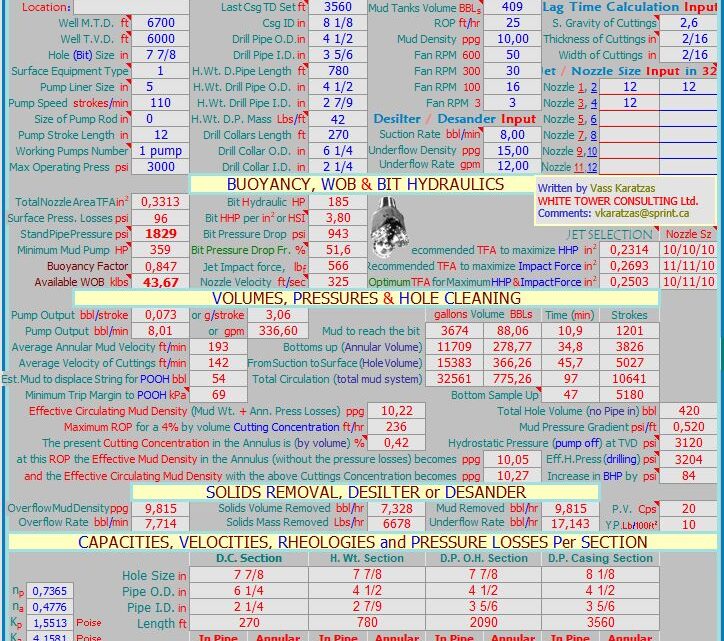
where gi = influx gradient, psi/ft; gmdp = mud gradient in drillpipe, psi/ft; and hi = influx height, ft. The influx gradient can be evaluated using the guidelines in Table 1.

It is necessary to calculate the mud weight needed to balance bottomhole formation pressure. “Kill-weight mud” is the amount of mud necessary to exactly balance formation pressure. It will be later shown that it is safer to use the exact required mud weight without variation

Because the drillpipe pressure has been defined as a bottomhole pressure gauge, the psidp can be used to calculate the mud weight necessary to kill the well. The kill mud formula follows:

Because the casing pressure does not appear in Eq. 2, a high casing pressure does not necessarily indicate a high kill-weight mud. The same is true for pit gain because it does not appear in Eq. 2. Example 1 uses the kill-weight mud formula.

Kverneland, Hege, Kyllingstad, Åge, and Magne Moe. "Development and Performance Testing of the Hex Mud Pump." Paper presented at the SPE/IADC Drilling Conference, Amsterdam, Netherlands, February 2003. doi: https://doi.org/10.2118/79831-MS