triplex mud pump output formula made in china

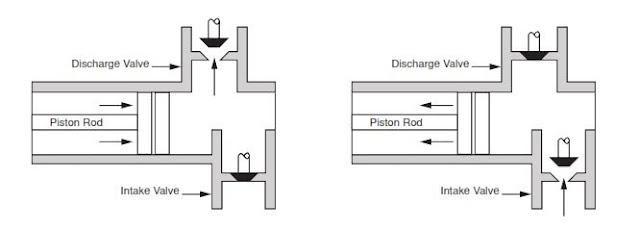
Rig pump output, normally in volume per stroke, of mud pumps on the rig is  one of important figures that we really need to know because we will use pump out put figures to calculate many parameters such as bottom up strokes,  wash out depth, tracking drilling fluid, etc. In this post, you will learn how to calculate pump out put for triplex pump and duplex pump in bothOilfield and Metric Unit.

Pump Output per Stroke (PO): The calculator returns the pump output per stroke in barrels (bbl).  However this can be automatically converted to other volume units (e.g. gallons or liters) via the pull-down menu.

A triplex mud (or slush) pump has three horizontal plungers (cylinders) driven off of one crankshaft. Triplex mud pumps are often used for oil drilling.

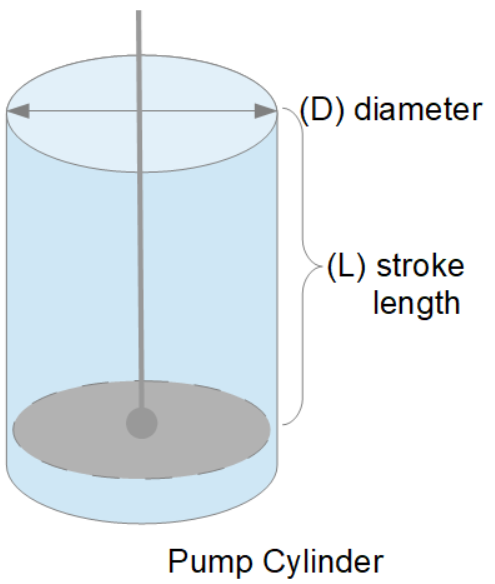
Oil and Gas drilling process - Pupm output for Triplex and Duplex pumpsTriplex Pump Formula 1 PO, bbl/stk = 0.000243 x ( in) E.xample: Determine the pump output, bbl/stk, at 100% efficiency for a 7" by 12". triplex pump: PO @ 100%,= 0.000243 x 7 x12 PO @ 100% = 0.142884bbl/stk Adjust the pump output for 95% efficiency: Decimal equivalent = 95 + 100 = 0.95 PO @ 95% = 0.142884bbl/stk x 0.95 PO @ 95% = 0.13574bbl/stk Formula 2 PO, gpm = [3(D x 0.7854)S]0.00411 x SPM where D = liner diameter, in. S = stroke length, in. SPM = strokes per minute Determine the pump output, gpm, for a 7" by 12". triplex pump at 80 strokes per minute: PO, gpm = [3(7 x 0.7854) 1210.00411 x 80 PO, gpm = 1385.4456 x 0.00411 x 80 PO = 455.5 gpm

Example:Duplex Pump Formula 1 0.000324 x (liner diameter, in) x ( stroke lengh, in) = ________ bbl/stk -0.000162 x (rod diameter, in) x ( stroke lengh, in) = ________ bbl/stk Pump out put @ 100% eff = ________bbl/stk Example: Determine the output, bbl/stk, of a 5 1/2" by 14" duplex pump at 100% efficiency. Rod diameter = 2.0": 0.000324 x 5.5 x 14 = 0.137214bbl/stk -0.000162 x 2.0 x 14 = 0.009072bbl/stk Pump output @ 100% eff. = 0.128142bbl/stk Adjust pump output for 85% efficiency: Decimal equivalent = 85 100 = 0.85 PO@85%)= 0.128142bbl/stk x 0.85 PO@ 85% = 0.10892bbl/stk Formula 2

PO. bbl/stk = 0.000162 x S[2(D) - d] where S = stroke length, in. D = liner diameter, in. d = rod diameter, in. Example: Determine the output, bbl/stk, of a 5 1/2". by 14". duplex pump @ 100% efficiency. Rod diameter = 2.0in.: PO@100%=0.000162 x 14 x [ 2 (5.5) - 2 ] PO @ 100%)= 0.000162 x 14 x 56.5 PO@ 100%)= 0.128142bbl/stk Adjust pump output for 85% efficiency: PO@85%,= 0.128142bb/stkx 0.85 PO@8.5%= 0.10892bbl/stk Metric calculation Pump output, liter/min = pump output. liter/stk x pump speed, spm. S.I. units calculation Pump output, m/min = pump output, liter/stk x pump speed, spm. Mud Pumps Mud pumps drive the mud around the drilling system. Depending on liner size availability they can be set up to provide high pressure and low flow rate, or low pressure and high flow rate. Analysis of the application and running the Drill Bits hydraulics program will indicate which liners to recommend. Finding the specification of the mud pumps allows flow rate to be calculated from pump stroke rate, SPM. Information requiredo Pump manufacturer o Number of pumps o Liner size and gallons per revolution Weight As a drill bit cutting structure wears more weight will be required to achieve the same RoP in a homogenous formation. PDC wear flats, worn inserts and worn milled tooth teeth will make the bit drill less efficiently. Increase weight in increments of 2,000lbs approx. In general, weight should be applied before excessive rotary speed so that the cutting structure maintains a significant depth of cut to stabilise the bit and prevent whirl. If downhole weight measurements are available they can be used in combination with surface measurements to gain a more accurate representation of what is happening in the well bore.

This article will focus on understanding of MWD signal decoding which is transmitted via mud pulse telemetry since this method of transmission is the most widely used commercially in the world.

As a basic idea, one must know that transmitted MWD signal is a wave that travels through a medium. In this case, the medium is mud column inside the drill string to mud pumps. Decoding is about detecting the travelling wave and convert it into data stream to be presented as numerical or graphical display.

The signal is produced by downhole transmitter in the form of positive pulse or negative pulse. It travels up hole through mud channel and received on the surface by pressure sensor. From this sensor, electrical signal is passed to surface computer via electrical cable.

Noise sources are bit, drill string vibration, bottom hole assemblies, signal reflection and mud pumps. Other than the noises, the signal is also dampened by the mud which make the signal becomes weak at the time it reaches the pressure sensor. Depth also weaken the signal strength, the deeper the depth, the weaker the signal detected.

Rock bit may create tri-lobe pattern. This pattern is created by the cones of the bit on the bottom of the hole. While drilling, the bit’s cones ride along this tri-lobe pattern and makes the bit bounce or known as axial vibration. As the bit bounces, back pressure is produced at the bit nozzles and transmitted to surface. The frequency of the noise created by bit bounce correlates with bit RPM. The formula to calculate its frequency is 3*(bit RPM)/60. When the bit bounce frequency match with MWD signal frequency, decoding is affected.

BHA components that have moving mechanical parts such as positive mud motor and agitator create noise at certain frequency. The frequency produced by these assemblies depends on the flow rate and the lobe configuration. The higher the flow rate and the higher the lobe configuration creates higher noise frequency.

Thruster, normally made up above MWD tool, tends to dampen the MWD signal significantly. It has a nozzle to use mud hydraulic power to push its spline mandrel – and then push the BHA components beneath it including the bit – against bottom of the hole. When the MWD signal is passing through the nozzle, the signal loses some of its energy. Weaker signal will then be detected on surface.

The common sources of signal reflection are pipe bending, change in pipe inner diameter or closed valve. These are easily found in pipe manifold on the rig floor. To avoid the signal reflection problem, the pressure sensor must be mounted in a free reflection source area, for example close to mud pumps. The most effective way to solve this problem is using dual pressure sensors method.

Mud pump is positive displacement pump. It uses pistons in triplex or duplex configuration. As the piston pushes the mud out of pump, pressure spikes created. When the piston retracts, the pressure back to idle. The back and forth action of pistons produce pressure fluctuation at the pump outlet.

Pressure fluctuation is dampened by a dampener which is located at the pump outlet. It is a big rounded metal filled with nitrogen gas and separated by a membrane from the mud output. When the piston pushes the mud the nitrogen gas in the dampener will be compressed storing the pressure energy; and when the piston retracts the compressed nitrogen gas in the dampener release the stored energy. So that the output pressure will be stable – no pressure fluctuation.

The dampener needs to be charged by adding nitrogen gas to certain pressure. If the nitrogen pressure is not at the right pressure, either too high or too low, the pump output pressure fluctuation will not be stabilized. This pressure fluctuation may match the MWD frequency signal and hence it disturbs decoding, it is called pump noise.

When the pump noise occurs, one may simply change the flow rate (stroke rate) so that the pump noise frequency fall outside the MWD frequency band – and then apply band pass frequency to the decoder.

The formula to calculate pump noise frequency is 3*(pump stroke rate)/60 for triplex pump and 2*(pump stroke rate)/60 for duplex pump. The rule of thumb to set up dampener pressure charge is a third (1/3) of the working standpipe pressure.

Sometime the MWD signal is not detected at all when making surface test although the MWD tool is working perfectly. This happen whenever the stand pipe pressure is the same with the pump dampener pressure. Reducing or increasing test flow rate to reduce or increase stand pipe pressure helps to overcome the problem.

When the MWD signal wave travels through mud as the transmission medium, the wave loses its energy. In other words, the wave is giving some energy to the mud.

The mud properties that are affecting MWD signal transmission is viscosity and weight. The increasing mud weight means there is more solid material or heavier material in the mud. Sometimes the mud weight increment is directly affecting mud viscosity to become higher. The MWD signal wave interacts with those materials and thus its energy is reduced on its way to surface. The more viscous the mud and the heavier the mud, the weaker the signal detected on surface.

Aerated mud often used in underbalance drilling to keep mud influx into the formation as low as possible. The gas injected into the mud acts as signal dampener as gas bubble is compressible. MWD signal suffers severely in this type of mud.

Proper planning before setting the MWD pulser gap, flow rate and pump dampener pressure based on mud properties information is the key to overcome weak signal.

The further the signal travels, the weaker the signal detected on the surface. The amount of detected signal weakness ratio compare to the original signal strength when it is created at the pulser depends on many factors, for example, mud properties, BHA component, temperature and surface equipment settings.

When two (or more) pumps are arranged in serial their resulting pump performance curve is obtained by adding theirheads at the same flow rate as indicated in the figure below.

Centrifugal pumps in series are used to overcome larger system head loss than one pump can handle alone. for two identical pumps in series the head will be twice the head of a single pump at the same flow rate - as indicated with point 2.

With a constant flowrate the combined head moves from 1 to 2 - BUTin practice the combined head and flow rate moves along the system curve to point 3. point 3 is where the system operates with both pumps running

When two or more pumps are arranged in parallel their resulting performance curve is obtained by adding the pumps flow rates at the same head as indicated in the figure below.

Centrifugal pumps in parallel are used to overcome larger volume flows than one pump can handle alone. for two identical pumps in parallel and the head kept constant - the flow rate doubles compared to a single pump as indicated with point 2

Note! In practice the combined head and volume flow moves along the system curve as indicated from 1 to 3. point 3 is where the system operates with both pumps running

In practice, if one of the pumps in parallel or series stops, the operation point moves along the system resistance curve from point 3 to point 1 - the head and flow rate are decreased.

[0003] A kick can be defined as a well control problem in which the pressure found within the drilled formation is greater than the mud or fluid hydrostatic pressure acting on the borehole or face of the formation. This formation pressure causes fluids to flow from the formation into the well bore. In almost all drilling operations, the operator attempts to maintain a hydrostatic pressure greater than the formation pressure and thus prevent kicks. On occasion, however, and for various reasons, the formation pressure exceeds the mud pressure and a kick will occur. Kicks have become even more common due to the present trend of increasing drilling rates by using lighter drilling mud.

[0006] FLOW RATE CHANGE - An increase in the flow-out or flow rate leaving the well while pumping at a constant rate is one of the primary kick indicators. The increased flow rate is interpreted to mean that the formation is forcing formation fluids into the well bore. A decrease in the flow rate exiting from the well while pumping at a constant rate is an indicator of lost circulation.

[0007] FLOWING WELL WITH PUMPS OFF - When the rig pumps are not moving the mud, a continued flow-out from the well indicates that a kick is in progress. An exception to this indicator is when the mud in the drill pipe is considerably heavier than that in the annulus, as in the case of a slug.

[0008] PIT VOLUME CHANGE - If the volume of fluid in the pits is not changed as a result of surface controlled actions, an increase in pit volume indicates that a kick is occurring. The fluids entering the well bore as a result of the kick displace an equal volume of mud at the flow line and result in a pit gain. A decrease in pit volume under these conditions indicates lost circulation.

[0012] Presently, flow-in measurement is based on the number of strokes per minute of triplex mud pumps (see Fig. 1). The flow race obtained from the pump strokes is then corrected by a volumetric pump efficiency. This pump efficiency can fluctuate between 80% to 95% accounting for inaccuracies of plus or minus seven and one half percent in the flow-in measurement.

[0014] Using the pump strokes and the paddle measurement for flow-in and flow-out respectively, the best accuracy for the differential flow over the entire fluid flow range cannot be much better than about twenty-five percent, or three hundred (GPM) in twelve hundred GPM. This is more than ten times the required accuracy, rendering prior methods of differential flow rate measurement inadequate for desired kick detection.

[0015] Electromagnetic flow meters have also been used but have drawbacks. They do not work in oil based muds (conductivity too low). They require complete modification of the return line. In offshore rigs where modification of the return line is difficult and space is limited, there is usually no way to install them. They require expensive maintenance to sustain their accuracy.

[0019] Further, U.S. Patent No. 4,754,641 to Orban et al., while providing improved results relative to the other methods for measuring fluid flow in return lines, still suffers from inaccuracies due to the requirement of a velocity probe which is inherently inaccurate in measuring mud flow in a drilling rig return line due to the wide range of elements in the mud. Thus, even with this advance, the art does not provide a method for sufficiently accurately determining a volumetric fluid flow rate such that a kick or lost circulation determination can be made in real time on a drilling rig.

[0024] In accord with the objects of the invention, improved methods and systems are disclosed for use in a return line system of a drilling rig to aid in accurately determining a volumetric flow rate of mud in the return line without the aid of a direct velocity measurement means. The system invention broadly comprises: a non-intrusive level sensor located in or in proximity to the return line for sensing the height or level of the mud flowing in the return line and providing a signal indicative thereof; and a processor responsive to the level sensor signals for determining, in conjunction with knowledge of the return line configuration and mud parameters, the flow-out rate of the mud. Where the level sensor is acoustic, the system also includes a multiple of correction sensors for determining the temperature gradient in the return line and for investigating the presence of gas in the return line, and for providing signals indicative thereof to the processor which is responsive thereto. A more complete system also includes calibration means for calibrating the flow-out rate with the flow-in rate, and means responsive to the calibration means for determining an undesirable condition such as a kick or fluid loss. Where the system is to be used on a rig which is subject to movement (e.g. a floating rig), angle and position sensors are also employed.

[0025] In accord with other objects of the invention, the level sensor is installed in a chimney which extends from the flow line and which is in close enough proximity to the bell nipple (e.g. less than 10 feet away) such that the mud level is high and the friction between the mud which is in supercritical flow and the flow line is kept small. Where the level sensor utilized is an ultrasonic pulse echo transceiver, the correction sensors include a plurality of temperature sensors at different height locations (e.g. near the mud, at the junction of the return line and a chimney in which the transceiver is mounted, and near the transceiver), to provide information regarding the temperature gradient in the return line, as well as a calibration target which acts to sense a change in sound velocity due to the presence of gas in the return line. Data from the temperature sensors and calibration target help provide a determination of the speed of sound in the air (or air/gas) above the mud such that the echo time measured by the ultrasonic transceiver can be properly correlated to a distance between the transceiver and the mud surface. By knowing the shape and size of the return line, the slope of the return line, the height of the fluid in the return line, and a mud parameter such as the viscosity/density ratio, an accurate flow-out determination can be made without the use of a direct velocity sensor. Where the slope of the return line is changing (as determined by the angle sensor) due to movement of the rig, the flow-out results can be corrected to compensate for the motion. The flow-out determinations are calibrated against the flow-in measurements which are made by detecting mud pump strokes (the positive displacement per pump stroke being known).

[0027] FIG. 1 is a schematic view of a drilling fluid or "mud" circulation system for a floating or fixed drilling rig where a flow measuring system embodying the invention may be used;

[0035] FIGS. 7a and 7b are logs of the flow-in of mud-displacing cement into a well-bore as measured from a cement truck, and the volumetric flow-out therefrom as measured by the system of the invention, respectively.

[0037] Referring to Fig. 1, a floating or fixed drilling rig mud circulation system is schematically illustrated, and it will be appreciated that the invention may be used with a bottom supported offshore drilling rig or a land drilling rig, as well as with a floating rig. As discussed above, flow rate into the well may be derived by counting the strokes per minute of mud pumps 16 or by direct measurement with a flow meter. After the "mud" or drilling fluid travels down the drill string 18, it moves up the annulus 20 between the casing 22 and the drill string 18 to the bell nipple 24. A return line 26 communicates with the bell nipple 24, as best shown in Figs. 1 and 2a, to return the mud to the mud pits 28. The flow-out measuring sensor system S according to the invention is disposed in the return line 26 in relative close proximity to the bell nipple 24; preferably within ten feet thereof.

[0038] The sensor system S in cooperation with a computer 14, which by way of example only includes a disk memory 28, a RAM memory 30, a CPU 32, and a ROM memory 34 (see Fig. 2a), is provided to accurately measure in real time the flow Q through return line 26. The volumetric flow Q is simply the product of the cross-sectional area A of fluid flowing at a given location in the line and the average velocity of the fluid moving at that location. However, because a determination of velocity is not made with a velocity probe, as most velocity probes are either intrusive or cannot handle the wide range of mud rheology, cuttings, gas, etc., the determination is made in the following manner,

[0039] In a simple return line geometry such as that seen in Fig. 2a, the velocity of mud in the annulus 20 is typically between one-half and one ft/sec, whereas the velocity of the mud in the return line 26 is typically between five and ten ft/sec. The acceleration of the mud is due to gravity and the slope of the return line, with the slope being great enough (e.g. typically greater than .5 degrees) to overcome the retarding effects of friction between the fluid and the pipe wall. In fact, most return lines have a slope of between two and twenty degrees. Under these conditions, a "critical flow" is established in the bell nipple, with the mud having a depth Hc and velocity Vc as seen in Fig. 2b. As the flow accelerates down the return line, the mud is in supercritical flow, and the velocity increases and the mud depth decreases, as is seen in Fig. 2b. This condition continues until the friction loss increases enough to offset the gravitational forces causing the acceleration. However, most return lines are too short for this equilibrium to be reached.

[0040] The inventors have found that in a typical return line with mud in supercritical flow, an increase of flow typically translates into an increase in mud depth (level) according to a substantially linear relationship for flow rates above about two hundred gallons per minute (200 GPM). Put another way, and as seen in Fig. 4 which shows the relationship between flow rate, mud level, and velocity in a return line, mud velocity is almost constant above 200 GPM, and an increase in flow rate directly translates into an increase in mud depth. Thus, for any given return line configuration with typical flow rates, the measured height of the mud in the return line may be calibrated to a flow race with reasonable accuracy. By way of example, the measurements indicated in Figure 4, which relate level to flow, were made three feet from the bell nipple in a return line of twelve inch diameter and five degree slope, and a mud with a density of twelve PPG and viscosity of ten cp. For return lines of different diameter or slope, mud of a different viscosity/density ratio, and a measurement location of different distance from the bell nipple, the curves of Figure 4 would assume different values.

[0041] As stated above, a review of Fig. 4 indicates that the GPM flow-out can be determined directly from the mud level without a determination of velocity. Thus, for the stated return line geometry and mud properties, a measured mud depth (or level) of 2.4 inches is equivalent to a mud flow-out of 300 GPM, while a measured mud depth of 4.8 inches is equivalent to a mud flow-out of 900 GPM. With a slope of 2.4"/600 GPM, in order to achieve a desired accuracy of the order of 25 GPM, a measurement of mud depth must be accurate to at least 0.1 inch.

[0042] Given the fact that flow rate can be measured directly from mud level if the return line geometry and mud makeup are known, means and methods for making the level measurement must be set forth. One preferred means for accomplishing the mud level measurement is seen in Fig. 2a where a sensor system mounts on the return line 26 and sits in an eight inch diameter hole cut into the return line. Sensor system S includes a chimney section 40 of six inch diameter in which the mud level sensor is mounted, and an inflatable seal 41 which fits around the chimney and inside pipe flanges 43 welded to the cut in the return line 26. For mechanical stability and alignment purposes, a support 45 is provided around chimney 40. Turnbuckles 46 connect the support to clamp 48 which grips the return line 26. This permits alignment of the sensor system S relative to the return line such that the sonic beam produced by a transceiver 50 (as discussed below) is substantially normal to the mud. In this arrangement, sonic beam reflections can be received and sensed by the transceiver 50.

[0044] The sensor system S includes a mud depth or level sensor for measuring the distance between the sensor and the mud surface. The sensor preferably includes an ultrasonic transmitter-receiver ("transceiver") 50 which both transmits and detects ultrasonic waves. Because a transceiver cannot detect a wave immediately after it has transmitted one (i.e. the transceiver has "dead time"), the transceiver 50 is preferably mounted in a housing or chimney 40 which removes the transceiver from the mud surface and causes the return signal to be received after the dead time. Mounting the transceiver 50 in the chimney 40 also protects it from mud splashing. Even so, a water sprayer 79 which receives water from water source 58 is preferably provided to clean the transceiver 50 and the other sensors located in or about chimney 40.

[0045] To convert the echo return time into a distance requires knowledge of the velocity of sound in the medium through which the sound pulse travels, as distance is equal to the product of time and velocity. Parameters affecting the velocity of sound include the temperature and the composition of the medium through which the sound travels. As the composition and the temperature of the "air" above the mud in the return line can change over time, additional sensors are utilized to monitor these parameters. For temperature, preferably three sensors 29a, 29b, and 29c are utilized to measure the heat gradient present between the mud surface and the transceiver 50. Thus, the first sensor 29a is placed on adjustable pole 52 and located near the mud. A second sensor 29b is located at the junction of the return line 26 and the chimney 40, while the third sensor 29c is located close to the transceiver 50. The sensors used are preferably AD590 solid state devices available from Analog Devices which produce exactly 1 microamp per degree Kelvin and are accurate enough to be calibrated electrically.

[0046] A manner for compensating the determined echo time for temperature gradients and changes therein is found in U.S. Patent #4,754,641 and will not be further discussed herein. It should suffice to note that all temperature determinations are fed via signal conditioners 57 and A/D converter 59 to the computer or processor means 14 which utilizes the temperature and echo time information in providing a distance, and hence a return line mud height determination. It should also be noted that similar techniques can be used with fewer or greater numbers of temperature sensors to provide more or less accuracy, and it is not the intent hereof to be limited to exactly three temperature sensors.

[0047] In taking into account the composition of the medium through which the sound is travelling, it is not necessary to determine the actual composition. Rather, it is only necessary to have a reference from which relative changes can be calculated. In particular, the provision of a reference target 51 on adjustable pole 52 at a known distance from the transceiver 50 permits a determination of the time it takes for the ultrasonic waves to travel a fixed distance at the temperatures provided by the temperature sensors 29a and 29b in whatever medium is present (e.g. air, gas, or air/gas mixture). Thus, by first sensing the reference echo time from transceiver 50 to target 51 and back to transceiver 50, and then sensing the echo time from transceiver 50 to the mud surface and back to the transceiver 50, the reference echo time can be used in conjunction with the temperature information to determine the distance between the transceiver 50 and the mud surface in an extremely accurate manner.

where Vs is the sonic velocity, Ta, Tm, and Tt are respectively the absolute temperature, the mean temperature of the mud path and the mean temperature of the target path, K is the effect of the gas composition on the sonic velocity, Lm is the distance from the transceiver 50 to the mud surface in the return line, Lt is the distance from the transceiver to the target, and △Tm and △Tt are the mud echo and target echo times respectively.

which indicates that with the reference target, the distance to the mud surface is derived from measurable (△Tm, △Tt, Tm, Tt) or known (Lt) parameters and is not dependent on the composition effect K of the gas. It should be noted that Tm and Tt as provided represent the mean of the gradient over distances Lm and Lt respectively, and that more complex representations more specifically accounting for temperature gradients would suggest themselves to those skilled in the arts.

[0050] Although knowing the actual composition of the medium through which the sound pulses travel is not necessary in practicing the present invention, it has been found that the method and apparatus of the present invention can be used effectively to detect the presence of methane gas (CH₄) in the mud return line and to calculate an approximate volumetric fraction of methane. Specifically, since the speed of sound in "air" (nitrogen/oxygen mixture) is approximately 332 m/sec at 0°C while the speed of sound in methane is approximately 430 m/sec., a large change in the speed of sound measurement derived from the target signal may properly be interpreted to indicate the introduction of methane into the return line since methane is by far the most abundant gas encountered during a drilling operation.

[0053] In order to obtain both target and mud echo information, the target 51 should be located in the return line such that the echoes received from the target do not interfere with the echoes received from the mud surface. In return lines of different diameters, the location might need to be different to avoid the second echo of the target. The placement of the target 51 on the adjustable pole 52 permits such adjustment and ensures that the target can be located at a location of more than half the distance from the transceiver to the mud surface. Alternatively, if desired, the sensing of the target and mud echoes can be time multiplexed. Also, if desired, automatic adjustment of transceiver transmission frequency in order to obtain the largest echo signals available can be provided by having microprocessor 61 which controls sensor 50 conduct a search for the best frequency.

[0054] Once the distance between the transceiver 50 and the mud surface (and the distance between the transceiver and the pipe or sediment surface of an "empty" pipe which may be determined by using the sensor system or through a knowledge of the pipe diameter etc.) is determined by the computer 14, a direct determination of flow rate may be obtained from a look-up table representing the mud height to flow rate relationship for the particular return line and mud parameters. Such a look-up table is generated either by accumulating experimental data or according to the following theoretical analysis.

[0055] Flow rate (Q) may be defined as the mathematical product of fluid velocity (V) and the cross-sectional flow area of the mud (A); i.e. Q = VA. The cross-sectional flow area of the mud is simply a function of the mud level and the geometry of return line. Complicating factors such as the presence of sediment 87 (as seen in Fig. 3) may also be taken into account, such as discussed in U.S. Patent #4,754,641. The sediment level may be determined in the absence of flowing mud. It is assumed that the sediment is simply stationary material which is taking up some of the cross-sectional area of the return line. While the resulting geometry of the fluid flow is not a simple one, it is nevertheless within the knowledge of those skilled in the art to solve for the cross-sectional flow area.

[0056] A determination of average fluid velocity (V) is not as straight-forward as the determination of cross-sectional area, particularly because the determination is not a direct one (i.e. no velocity sensors are used). With a simple return line geometry and no friction, the velocity of the mud would be a direct result of the vertical fall of the liquid surface; the energy of which would be converted from potential to kinetic energy. In particular, such a system could be described according to the following relationships:

where Vc is the critical velocity, g is the acceleration due to gravity, Ac is the critical cross-sectional area of the mud in the return line close to the junction of the return line with the bell nipple (i.e. the critical area), and b is the surface width of the fluid. For a given mud flow rate Q and geometry which relates Ac and b, the critical velocity Vc, the critical area Ac, and the critical depth hc become known. As a result, tables can be generated which relate various flow rates Q and resulting values of Vc, Ac and hc.

[0058] While relationships (5) - (10) assume the absence of friction up to the critical point, it will be appreciated that friction does play a role in the velocity of the mud in the return line, and accounting for friction is necessary. The following conservation of energy equation makes such an account:

[0059] With the provided continuity (6) and critical flow (10) equations and with the provided energy equation (11), the velocity V at the location of the level sensor can be determined as long as the friction factor f can be found. The friction factor f can be determined according to the Reynold"s number Re pursuant to well known equations. The Reynold"s number, in turn, is dependent on the velocity, hydraulic diameter, density and viscosity of the flowing fluid according to Re = VDρ/µ. The density and viscosity are typically monitored on the job site and are available. Account, however, should be taken if the viscosity or density changes significantly over time. By keeping the location of the level sensor near the bell nipple, a crude estimate of friction is sufficient, as the inventors have determined that within approximately ten feet of the bell nipple, the friction losses of the returning fluid are small and that a crude estimate yields reasonable results. In fact, Re and f are considered to be constant and equal to their critical values throughout the length of the return line (although the critical values may change over time if the flow or mud parameters change). This is a reasonable approximation for as the velocity increases, the depth decreases, tending to keep Re constant. A typical friction loss of about twenty percent yields a velocity reduction of about ten percent, and an error of ten percent in analyzing the friction losses would result in a tolerable change of velocity of only one percent. Regardless of how the friction loss determination is originally estimated, calibration of flow-out corrects for any inaccuracies as is hereinafter described. In sum, then, equations (5) - (11) are solved at the outset of a job for the fixed values of the pipe size D, distance between the sensor system S and the bell nipple L, return line slope ϑ, mud viscosity µ, and mud density ρ, to establish the height (h) to flow (Q) look-up table appropriate for the job.

[0060] Turning to Figure 5, the method for determining the flow rate in the return line, which utilizes calibration is seen. At 100 the echo times for the reference target and for the mud surface are measured, along with the temperature gradient in the return line and chimney as measured by the temperature sensors. Also, as will be discussed hereinafter, the flow into the well is measured. In a preferred embodiment, the angle of the return line, and the density and viscosity of the mud are further measured. At 104, the echo times and temperature gradient are used to find the fluid flow height H. Also, at 104 the mud viscosity and density are used in conjunction with parameters stored at 200 such as the return line geometry (e.g. diameter), the horizontal distance from the bell nipple to the measurement location (L), the return line slope (ϑ), the gravitational constant (g), and any other relevant parameters which are constant for the given system, to provide a determination of the velocity of the mud in the return line at the measurement location in accord with equations (4) through (11) above. From the fluid flow height, the cross-sectional area of the mud in the return line at the measurement location is determined at 104. If available, additional information such as sediment level (box 107) may be provided to the processor which determines at 104 the cross-sectional area of the mud.

[0061] At 110, a determination of the flow-out (Q) of the mud from the wellbore is obtained from a transform (i.e. look-up table such as is represented by Fig. 4 for the provided return line and mud parameters) which relates the flow height to flow-out. Alternatively, the flow-out (Q) is found as the product of the determined cross-sectional area (A) of the mud and the mud velocity (V) at the measurement location. The flow-out (Q) determination at 110, however, is preferably viewed as a theoretical flow-out, such that through a calibration, an absolute flow-out determination (which is only absolute relative to the accuracy of the flow-in pump measurements) can be made. Thus, at start-up a single or multi-point calibration lasting only several minutes is preferably performed, and provides a calibration between the actual flow-out and the "estimated" theoretical flow out. The calibration accounts for non-linearity, errors in estimating friction, and other systematic errors which may be present such as changes in geometry, mud properties, sensor calibration, etc. Then, during drilling, when the theoretical flow-out determination is made at 110, the flow-out determination is corrected at 112 by the calibration constant calculated at start up.

[0062] The corrected flow-out determination is subjected to a trend analysis where the flow-out determination of 112 is compared at 118 continuously to the flow-in measurement measured by the positive displacement mud pump strokes at step 100 to determine whether there is any difference between the two. Where there is a difference, that difference is monitored at 119 over time to determine whether the difference is relatively constant over time. If the difference is relatively constant (i.e. steady or slowly changing) it is assumed that the flow-in or flow-out calibration has drifted and an average calibration coefficient (over a period of about an hour) is determined at 120 and fed back to the calibration correction step 112; i.e. autocalibration. If the difference between flow-out and flow-in (ΔQ) is not relatively constant, a determination is made at 122 as to whether the rate of change is greater than or equal to 10 GPM/Min over a four minute time scan. If the rate of change is less than 10GPM/Min (as seen in Fig. 6a) noise or measurement drift is assumed, and the situation is accommodated via autocalibration. If the rate of change is greater than 10 GPM/Min a warning is given, and if it lasts for four minutes, as seen in Fig. 6b, an alarm is sounded by gauge 62 (of Fig. 2) and an influx (kick) or an outflux (fluid loss) situation is declared at 125. Regardless, the flow-out, and delta flow determinations are preferably recorded at recorder 60 (of Fig. 2) in a log format over time.

[0064] Testing the system and method inventions during a cementing operation where the flow-in was carefully measured independently by the cement truck pumps (not by the rig mud pumps), it was determined that the system and method inventions provide an excellent determination of flow-out. As seen in Figs. 7a and 7b, during a period of slightly over an hour, the measured flow-out (Fig. 7b) tracked the known flow-in (Fig. 7a) accurately. In fact, the total volume of cement and mud that was used during the hour as measured by the cement truck was two hundred seven barrels, while the measured (via integration) displaced out-flow was two hundred one barrels; a very acceptable difference of only three percent.

[0065] There have been described and illustrated herein systems and methods for measuring the volumetric flow of a fluid in a return line. While particular embodiments have been illustrated and described, it is not an intention that the invention be limited thereto, as it is intended that the invention be as broad in scope as the art will allow. For example, while a system was described as having three temperature sensors, and a reference target for "sensing" a change in medium above the mud, it will be appreciated by those skilled in the art that the sensors and reference target are employed for compensating the transceiver echo time for a changed speed of sound, and that other correction means could be utilized. Also, while the system was described as using an ultrasonic transceiver, equivalents of the same, including separate transmitters and receivers, could easily be utilized. In fact, if desired, the ultrasonic transceiver as well as the temperature sensors and reference target may all be replaced by an optic or radar system which could accurately sense the height of the mud in the return line. Further, while the sensor system is preferably located within ten feet of the bell nipple in order to minimize the effect of friction, it will be appreciated that it is still possible to locate the sensor system beyond that distance if account is taken of friction in accord with the technical discussion provided herein with reference to Reynold"s numbers etc., or if account is taken of friction through calibration. Therefore, it will be apparent to those skilled in the art that yet other changes and modifications may be made to the invention as described without departing from the scope and spirit of the invention as so claimed.

The feasibility of applying delay pressure detection method to eliminate mud pump pressure interference on the downhole mud pressure signals is studied. Two pressure sensors mounted on the mud pipe in some distance apart are provided to detect the downhole mud continuous pressure wave signals on the surface according to the delayed time produced by mud pressure wave transmitting between the two sensors. A mathematical model of delay pressure detection is built by analysis of transmission path between mud pump pressure interference and downhole mud pressure signals. Considering pressure signal transmission characteristics of the mud pipe, a mathematical model of ideal low-pass filter for limited frequency band signal is introduced to study the pole frequency impact on the signal reconstruction and the constraints of pressure sensor distance are obtained by pole frequencies analysis. Theoretical calculation and numerical simulation show that the method can effectively eliminate mud pump pressure interference and the downhole mud continuous pressure wave signals can be reconstructed successfully with a significant improvement in signal-to-noise ratio (SNR) in the condition of satisfying the constraints of pressure sensor distance.

In measurement while drilling (MWD), various downhole signals will be transmitted to the surface in real time for instructing the drilling operation. One of the most common methods of transmitting the measured downhole information to the surface is through mud pressure pulses produced by mechanical modulation of a mud siren in MWD tools and transmitted at acoustic speed in the mud flow. The mud siren generates mud continuous pressure wave signals with complex modulation methods to produce higher data rates. When transmitting the mud pressure signals, there will be a lot of pressure noise and interference, among which the mud pressure fluctuation generated by the mud pump contributes to the largest influence. The mud pump pressure interference is related to the pump stoke rate which includes fundamental component and harmonic component. When the mud pump is in imbalance operation mode caused by sealing problem or in abnormal working status, some higher harmonic amplitude will become very large. Although the pressure dampers are equipped on mud pump pipe, the pressure fluctuation generated by mud pump reaches or exceeds the downhole signal strength detected in the stand pipe [1]. These higher harmonics will enter the frequency band of mud pressure signal and thereby create great interference that cannot be eliminated by conventional signal processing method, leading to the great decrease of signal-to-noise ratio (SNR) of signal and affecting extraction of the MWD signals. Many studies had been done to eliminate the pump interference. Marsh and others proposed the matched filter method which treated mud pump interference as random noise and calculated the autocorrelation coefficient to eliminate the mud pump pressure interference [2]. However, the pump interference is a kind of system interference rather than random noise, so the conclusions of the method needed further discussion. Brandon and others proposed an adaptive compensation method which uses extracted interference component in the signal and automatically adjusts strength of the interference component to eliminate the pump pressure interference impact on the signal [3], but the effect was limited. Some literatures [4–7] introduced the delay pressure detection technique and built a mathematical model, being fitted to the single-frequency signal with pressure sensors distance of quarter signal wavelength, for eliminating the mud pump pressure interference. Because components of many frequencies are contained in mud continuous pressure wave signals, the mathematical model presented in those literatures cannot be applied in reconstruction of actual mud continuous pressure wave signals. Based on transmission path analysis of mud pump pressure interference and downhole mud pressure signals, the authors established the mathematical model in time domain for processing mud continuous pressure wave signals according to the fundamental mathematical principle of delay pressure detection method and then studied the reconstruction method of mud continuous wave signals in both time domain and frequency domain and constraints of the distance between pressure sensors.

The delay pressure detection method uses two pressure sensors being some distance apart on the mud pipe to detect and process the mud pressure signal; Figure 1 shows the schematic figure of mud pressure signal detection system. Two pressure sensors, A and B, having distance between each other, are equipped in a straight pipe between wellhead and mud pump. The pressure signals received by two sensors contain downhole signal (mud pressure signal) , downhole random noise , and mud pump pressure interference . The transmission direction of pump pressure interference is opposite to that of downhole signal. Suppose that the propagation velocity of the mud pressure wave is and the pressure wave transmission time between sensors A and B is .

Considering that the maximum frequency of mud continuous pressure wave signal in transmission will be dozens of hertz (Hz), the signal frequency is lower and limited. In limited frequency band, the signal attenuation in amplitude will keep unchangeable when mud continuous pressure wave signal passes the straight pipe between pressure sensors A and B, so the pipe can be seen as an undistorted transmission system and regarded as an ideal low-pass filter. The frequency domain transfer function of the system can be described as

According to digital filter theory, is a -order infinite impulse response (IIR) filter system [10] and its frequency domain response, being similar to the low-pass filter with sharp cut-off characteristic, strengthens with . When is an ideal low-pass transmission, the output of is a differential equation and can be expressed as

The straight pipe between pressure sensors A and B will cause pressure signal attenuation. According to the transmission characteristics of mud pressure wave [11], the attenuation coefficient of pressure signal or the amplitude ratio of mud pipe can be described as

where is the pipe length between pressure sensors A and B, is the attenuation index, is the volume fraction of gas in mud, is the volume fraction of solids in mud, is the bulk modulus of gas in mud, is the bulk modulus of liquid in mud, is the bulk modulus of solid in mud, is the bulk modulus of the mud pipe, is the internal diameter of the mud pipe, is the wall thickness of the mud pipe, is the Poisson’s ratio of the mud pipe, is the kinematic viscosity of mud, and is signal frequency.

Suppose that the mud is water-based mud. The computational conditions are listed as follows [12]: internal diameter of the mud pipe is 108.6 mm, wall thickness of the mud pipe is 9.2 mm, the mud kinematic viscosity is 20 mPa·, the pipe Poisson’s ratio is 0.3, volume fraction of gas in mud is 0.5%, volume fraction of solid in mud is 15%, the mud pipe bulk modulus is 210 GPa, and bulk modulus of water in mud is 2.04 GPa, bulk modulus of solid in mud is 16.2 GPa. If signal frequency of mud continuous pressure wave is , when the distance between pressure sensors A and B is less than , the pressure signal attenuation coefficient will be by numerical calculation. This means that transmission loss of mud pressure wave signal is very small and the attenuation coefficient will be close to 1 when the two sensors are nearer to each other.

If the maximum frequency of mud pressure signal spectrum is , there is . When the corresponding pole frequency falls into the passband of ideal low-pass filter, the pole frequency will be very likely to enter signal spectrum and generate great interference in the reconstruction of downhole signal. To avoid such situation, all the pole frequency values should be greater than the passband frequency of ideal low-pass filter. That is, .

Propagation velocity of the mud pressure wave in the mud pipe can be calculated according to the literature [13]. Take the mud pressure DPSK (differential phase shift keying) signal with carrier wave frequency of 24 Hz for example, the maximum frequency of signal spectrum is 36 Hz. When  Hz, we have  s. Furthermore, if the mud pressure wave velocity is  m/s, the corresponding distance between pressure sensors is  m.

The numerical simulation takes mud pressure DPSK signal as an example. According to the mathematical model of mud pressure DPSK signal [14], the signal can be formulated as . In the formula, carrier frequency is  Hz, signal amplitude is  Pa, and data code is . By analyzing the power spectral of mud pressure DPSK signal, the maximum frequency of signal spectrum is  Hz and the signal power is . Mud pump interference simulates multifrequency pressure pulsation generated by triplex pump with pump impulse rate 64 r/min, and the fundamental wave frequency is with harmonic orders 2 to 9. Therefore, the frequency changing range of pump interference is from to . Suppose that the fundamental wave and every harmonic wave amplitude are . The corresponding power density of fundamental wave or every harmonic wave is an impact function and the average power of the pump interference is

Figure 2 shows the signal waveform and the signal spectrum mixed with mud pump interference. It can be seen that the mud pressure DPSK signal is completely submerged in the pump interference in time domain and the signal spectrum is completely covered by mud pump interference frequencies.

Suppose that the signal acts on the at , has zero state response only, and the system output before is . Simulation result of the reconstructed signal by MATLAB programming is shown in Figure 3. It can be seen that the mud pump interference is eliminated after delay pressure detection from Figure 3(a); the reconstructed signal in Figures 3(b) and 3(c) are consistent with the mud pressure DPSK signal in Figure 2(a). In Figure 3(b), the numerical calculation result shows that the SNR of reconstructed mud pressure DPSK signal under condition of  ms is 72.4, which is about 657 times higher than that of existing pump interference. Numerical calculation and analysis show that the SNR of reconstructed mud pressure DPSK signal will be affected by the delayed time in time domain and the influence is listed in Table 1. The reason is that the set value of , participating in the recursive computation in (11), will be increased with the delayed time , but the influence is not notable. In Figure 3(c), the reconstructed mud pressure DPSK signal based on inverse Fourier transform method has no distortion in whole waveform and is better than the signal reconstructed by time-domain differential equation method in quality. However, both reconstruction methods can reconstruct downhole signal effectively.

(1) Theoretical analysis and numerical simulation show that delay pressure detection method can effectively eliminate mud pump interference and realize reconstruction or recovery of mud continuous pressure wave signals with greater SNR.

(3) According to the mathematical principle analysis of delay pressure detection method, it is only applied to eliminate special interference (mud pump pressure interference) whose transmitting direction is opposite to that of the downhole signal. For mud continuous pressure wave signal which is seriously affected by mud pump interference, this method has some inspiration effect on solving the problem of mud pump pressure interference.

A kick is a well control problem in which the pressure found within the drilled rock is higher than the mud hydrostatic pressure acting on the borehole or rock face. When this occurs, the greater formation pressure has a tendency to force formation fluids into the wellbore. This forced fluid flow is called a kick. If the flow is successfully controlled, the kick is considered to have been killed. An uncontrolled kick that increases in severity may result in what is known as a “blowout.”

Yet another factor affecting kick severity is the “pressure differential” involved. Pressure differential is the difference between the formation fluid pressure and the mud hydrostatic pressure. If the formation pressure is much greater than the hydrostatic pressure, a large negative differential pressure exists. If this negative differential pressure is coupled with high permeability and high porosity, a severe kick may occur.

Another way of labeling kicks is by identifying the required mud weight increase necessary to control the well and kill a potential blowout. For example, if a kick required a 0.7-lbm/gal (84-kg/m3) mud weight increase to control the well, the kick could be termed a 0.7-lbm/gal (84-kg/m3) kick. It is interesting to note that an average kick requires approximately 0.5 lbm/gal (60 kg/m3), or less, mud weight increase.

Kicks occur as a result of formation pressure being greater than mud hydrostatic pressure, which causes fluids to flow from the formation into the wellbore. In almost all drilling operations, the operator attempts to maintain a hydrostatic pressure greater than formation pressure and, thus, prevent kicks; however, on occasion the formation will exceed the mud pressure and a kick will occur. Reasons for this imbalance explain the key causes of kicks:

Insufficient mud weight is the predominant cause of kicks. A permeable zone is drilled while using a mud weight that exerts less pressure than the formation pressure within the zone. Because the formation pressure exceeds the wellbore pressure, fluids begin to flow from the formation into the wellbore and the kick occurs.

These abnormal formation pressures are often associated with causes for kicks. Abnormal formation pressures are greater pressures than in normal conditions. In well control situations, formation pressures greater than normal are the biggest concern. Because a normal formation pressure is equal to a full column of native water, abnormally pressured formations exert more pressure than a full water column. If abnormally pressured formations are encountered while drilling with mud weights insufficient to control the zone, a potential kick situation has developed. Whether or not the kick occurs depends on the permeability and porosity of the rock. A number of abnormal pressure indicators can be used to estimate formation pressures so that kicks caused by insufficient mud weight are prevented (some are listed in Table 1).

An obvious solution to kicks caused by insufficient mud weights seems to be drilling with high mud weights; however, this is not always a viable solution. First, high mud weights may exceed the fracture mud weight of the formation and induce lost circulation. Second, mud weights in excess of the formation pressure may significantly reduce the penetration rates. Also, pipe sticking becomes a serious consideration when excessive mud weights are used. The best solution is to maintain a mud weight slightly greater than formation pressure until the mud weight begins to approach the fracture mud weight and, thus, requires an additional string of casing.

Improperly filling up of the hole during trips is another prominent cause of kicks. As the drillpipe is pulled out of the hole, the mud level falls because the pipe steel no longer displaces the mud. As the overall mud level decreases, the hole must be periodically filled up with mud to avoid reducing the hydrostatic pressure and, thereby, allowing a kick to occur.

Several methods can be used to fill up the hole, but each must be able to accurately measure the amount of mud required. It is not acceptable—under any condition—to allow a centrifugal pump to continuously fill up the hole from the suction pit because accurate mud-volume measurement with this sort of pump is impossible. The two acceptable methods most commonly used to maintain hole fill-up are the trip-tank method and the pump-stroke measurements method.

The trip-tank method has a calibration device that monitors the volume of mud entering the hole. The tank can be placed above the preventer to allow gravity to force mud into the annulus, or a centrifugal pump may pump mud into the annulus with the overflow returning to the trip tank. The advantages of the trip-tank method include that the hole remains full at all times, and an accurate measurement of the mud entering the hole is possible.

The other method of keeping a full hole—the pump-stroke measurement method—is to periodically fill up the hole with a positive-displacement pump. A flowline device can be installed with the positive-displacement pump to measure the pump strokes required to fill the hole. This device will automatically shut off the pump when the hole is full.

Gas-contaminated mud will occasionally cause a kick, although this is rare. The mud density reduction is usually caused by fluids from the core volume being cut and released into the mud system. As the gas is circulated to the surface, it expands and may reduce the overall hydrostatic pressure sufficient enough to allow a kick to occur.

Although the mud weight is cut severely at the surface, the hydrostatic pressure is not reduced significantly because most gas expansion occurs near the surface and not at the hole bottom.

Occasionally, kicks are caused by lost circulation. A decreased hydrostatic pressure occurs from a shorter mud column. When a kick occurs from lost circulation, the problem may become severe. A large volume of kick fluid may enter the hole before the rising mud level is observed at the surface. It is recommended that the hole be filled with some type of fluid to monitor fluid levels if lost circulation occurs.

An increase in flow rate leaving the well, while pumping at a constant rate, is a primary kick indicator. The increased flow rate is interpreted as the formation aiding the rig pumps by moving fluid up the annulus and forcing formation fluids into the wellbore.

If the pit volume is not changed as a result of surface-controlled actions, an increase indicates a kick is occurring. Fluids entering the wellbore displace an equal volume of mud at the flowline, resulting in pit gain.

When the rig pumps are not moving the mud, a continued flow from the well indicates a kick is in progress. An exception is when the mud in the drillpipe is considerably heavier than in the annulus, such as in the case of a slug.

A pump pressure change may indicate a kick. Initial fluid entry into the borehole may cause the mud to flocculate and temporarily increase the pump pressure. As the flow continues, the low-density influx will displace heavier drilling fluids, and the pump pressure may begin to decrease. As the fluid in the annulus becomes less dense, the mud in the drillpipe tends to fall and pump speed may increase.

Other drilling problems may also exhibit these signs. A hole in the pipe, called a “washout,” will cause pump pressure to decrease. A twist-off of the drillstring will give the same signs. It is proper procedure, however, to check for a kick if these signs are observed.

When the drillstring is pulled out of the hole, the mud level should decrease by a volume equivalent to the removed steel. If the hole does not require the calculated volume of mud to bring the mud level back to the surface, it is assumed a kick fluid has entered the hole and partially filled the displacement volume of the drillstring. Even though gas or salt water may have entered the hole, the well may not flow until enough fluid has entered to reduce the hydrostatic pressure below the formation pressure.

Drilling fluid provides a buoyant effect to the drillstring and reduces the actual pipe weight supported by the derrick. Heavier muds have a greater buoyant force than less dense muds. When a kick occurs, and low-density formation fluids begin to enter the borehole, the buoyant force of the mud system is reduced, and the string weight observed at the surface begins to increase.

Fortunately, the lower mud weights from the cuttings effect are found near the surface (generally because of gas expansion), and do not appreciably reduce mud density throughout the hole. Table 3 shows that gas cutting has a very small effect on bottomhole hydrostatic pressure.

An important point to remember about gas cutting is that, if the well did not kick within the time required to drill the gas zone and circulate the gas to the surface, only a small possibility exists that it will kick. Generally, gas cutting indicates that a formation has been drilled that contains gas. It does not mean that the mud weight must be increased.

The MWD tool enables monitoring of the acoustic properties of the annulus for early gas-influx detection. Pressure pulses generated by the MWD pulser are recorded and compared at the standpipe and the top of the annulus. Full-scale testing has shown that the presence of free gas in the annulus is detected by amplitude attenuation and phase delay between the two signals. For water-based mud systems, this technique has demonstrated the capacity to consistently detect gas influxes within minutes before significant expansion occurs. Further development is currently under way to improve the system’s capability to detect gas influxes in oil-based mud.

Some MWD tools feature kick detection through ultrasonic sensors. In these systems, an ultrasonic transducer emits a signal that is reflected off the formation and back to the sensor. Small quantities of free gas significantly alter the acoustic impedance of the mud. Automatic monitoring of these signals permits detection of gas in the annulus. It should be noted that these devices only detect the presence of gas at or below the MWD tool.

When a kick occurs, note the type of influx (gas, oil, or salt water) entering the wellbore. Remember that well-control procedures developed here ar