mud pump rpm calculator in stock

Rig pump output, normally in volume per stroke, of mud pumps on the rig is  one of important figures that we really need to know because we will use pump out put figures to calculate many parameters such as bottom up strokes,  wash out depth, tracking drilling fluid, etc. In this post, you will learn how to calculate pump out put for triplex pump and duplex pump in bothOilfield and Metric Unit.

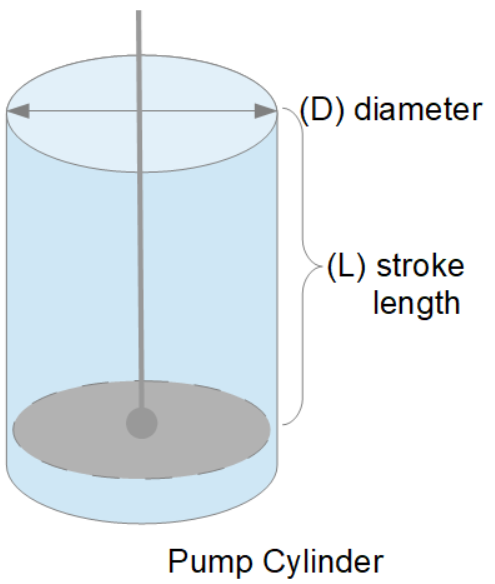
Pump Output per Stroke (PO): The calculator returns the pump output per stroke in barrels (bbl).  However this can be automatically converted to other volume units (e.g. gallons or liters) via the pull-down menu.

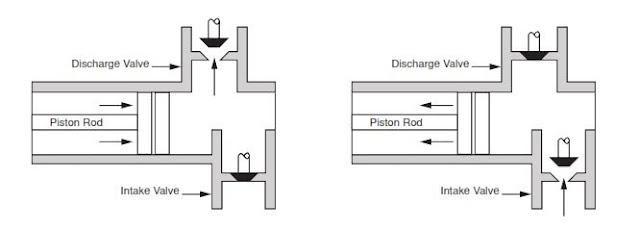
A triplex mud (or slush) pump has three horizontal plungers (cylinders) driven off of one crankshaft. Triplex mud pumps are often used for oil drilling.

The shaft power - the power required transferred from the motor to the shaft of the pump - depends on the efficiency of the pump and can be calculated as Ps(kW) = Ph(kW)/ η (3)

We provide hydraulic components & repair services for industrial applications like paper mills, saw mills, steel mills, recycling plants, oil & gas applications and mobile applications, including construction, utility, mining, agricultural and marine equipment. This includes hydraulic pumps, motors, valves, servo/prop valves, PTOs, cylinders & parts.

I understand that John Blue Company is furnishing this calculator "as is" and that it is not covered by any warranty whatsoever, whether express, implied, or statutory, including, but not limited to, its freedom from errors, its fitness for any particular purpose, and/or its correct or incorrect use. I agree that by using this calculator, I am doing so at my own risk. I agree to hold John Blue harmless for any and all damages directly or indirectly related to the use of this calculator. In no respect shall John Blue Company incur any liability for any damages, including, but not limited to, direct, indirect, special, or consequential damages arising out of, resulting from, or in any way connected to the use of this calculator, whether or not based upon warranty, contract, tort, or otherwise; whether or not injury was sustained by persons or property or otherwise; and whether or not loss was sustained from, or arose out of, the results of this calculator and its use.

Both the EMP40™ and PITPUMP™ feature advanced telematics for active health monitoring in support of proactive preventative maintenance programs. The variable pump speed of PITPUMP™ allows it to work seamlessly with the smart generator architecture of the EMPOWER™ line. Current job site use has resulted in decreased fuel consumption of over 40% when the EMP40™ is used in tandem with PITPUMP™ across both entry- and exit-side operations.

The purpose of this article is to present some guidelines and simplified techniques to size pumps and piping typically used in mud systems. If unusual circumstances exist such as unusually long or complicated pipe runs or if very heavy or viscous drilling muds are used, a qualified engineer should analyze the system in detail and calculate an exact solution.

To write about pumps, one must use words that are known and well understood. For example, the label on the lefthand side of any centrifugal pump curve is Total Head Feet. What does this mean?

Total Head remains constant for a particular pump operated at a constant speed regardless of the fluid being pumped. However, a pump’s pressure will increase as the fluid density (mud weight) increases according to the following relationship:

Note that the pump pressure almost doubled. It follows that the required pump horsepower has increased by the same percentage. If the pump required 50 HP for water service, it will require the following horsepower for 16 lb/gal mud:

To summarize, a pump’s Total Head remains constant for any fluid pumped, only the pump pressure and pump horsepower will change. Therefore, a pump motor must be sized according to the heaviest weight mud to be pumped.

In our example problem, the required desilter pressure head is 75 ft. for any mud weight. However, the pressure would be 30.3 PSIG for water or 43.6 PSIG for 12 lb mud or 58.1 PSIG for 16 lb mud. A good rule of thumb is that the required pressure (PSIG) equals 4 times the mud weight (12 LB/GAL x 4 = 48 PSIG).

Determine the required pressure head and flow rate. If the pump is to supply a device such as a mud mixing hopper or a desilter, consult the manufacturer’s information or sales representative to determine the optimum flow rate and pressure head required at the device. (On devices like desilters the pressure head losses downstream of the device are considered negligible and are usually disregarded.)

Select the basic pump to pump the desired flow rate. Its best to refer to a manufacturer’s pump curve for your particular pump. (See example – Figure 3).

The pump’s impeller may be machined to a smaller diameter to reduce its pressure for a given application. Refer to the manufacturer’s pump curves or manufacturer’s representative to determine the proper impeller diameter. Excessive pressure and flow should be avoided for the following reasons:

The pump must produce more than 75 FT-HD at the pump if 75 FT-HD is to be available at the desilter inlet and the pump’s capacity must be at least 800 GPM. Therefore, we should consider using one of the following pumps from the above list: 4″ x 5″ Pump 1750 RPM – 1000 GPM at 160 FT-HD; or 5″ x 6″ Pump 1750 RPM – 1200 GPM at 160 FT-HD.

The pump suction and discharge piping is generally the same diameter as the pump flange diameters. The resulting fluid velocities will then be within the recommended ranges of 4 to 10 FT/SEC for suction lines and 4 to 12 FT/

SEC for discharge lines. Circumstances may dictate that other pipe diameters be used, but remember to try to stay within the above velocity guidelines. Smaller pump discharge piping will create larger pressure drops in the piping

and the pump may not be able to pump the required amount of fluid. (For example, don’t use a 4″ discharge pipe on a 6″ x 8″ pump and expect the pump’s full fluid flow.)

6″ pipe may be used for the suction pipe since it is relatively short and straight and the pump suction is always flooded. 6″ pipe is fully acceptable for the discharge pipe and is a good choice since the desired header is probably 6″ pipe.

8″ pipe may be used for the suction pipe (V = 5.13 FT/SEC) since V is still greater than 4 FT/SEC. 8″ pipe would be preferred if the suction is long or the suction pit fluid level is low with respect to the pump.

Pumps tend to be one of the biggest energy consumers in industrial operations. Pump motors, specifically, require a lot of energy. For instance, a 2500 HP triplex pump used for frac jobs can consume almost 2000 kW of power, meaning a full day of fracking can cost several thousand dollars in energy costs alone!

So, naturally, operators should want to maximize energy efficiency to get the most for their money. Even a 1% improvement in efficiency can decrease annual pumping costs by tens of thousands of dollars. The payoff is worth the effort. And if you want to remotely control your pumps, you want to keep efficiency in mind.

In this post, we’ll point you in the right direction and discuss all things related to pump efficiency. We’ll conclude with several tips for how you can maintain pumping efficiency and keep your energy costs down as much as possible.

In simple terms, pump efficiency refers to the ratio of power out to power in. It’s the mechanical power input at the pump shaft, measured in horsepower (HP), compared to the hydraulic power of the liquid output, also measured in HP. For instance, if a pump requires 1000 HP to operate and produces 800 HP of hydraulic power, it would have an efficiency of 80%.

Remember: pumps have to be driven by something, i.e., an electric or diesel motor. True pump system efficiency needs to factor in the efficiency of both the motor AND the pump.

Consequently, we need to think about how electrical power (when using electric motors) or heat power (when using combustion engines) converts into liquid power to really understand pump efficiency.

Good pump efficiency depends, of course, on pump type and size. High-quality pumps that are well-maintained can achieve efficiencies of 90% or higher, while smaller pumps tend to be less efficient. In general, if you take good care of your pumps, you should be able to achieve 70-90% pump efficiency.

Now that we have a better understanding of the pump efficiency metric, let’s talk about how to calculate it. The mechanical power of the pump, or the input power, is a property of the pump itself and will be documented during the pump setup. The output power, or hydraulic power, is calculated as the liquid flow rate multiplied by the "total head" of the system.

IMPORTANT: to calculate true head, you also need to factor in the work the pump does to move fluid from the source. For example, if the source water is below the pump, you need to account for the extra work the pump puts in to draw source water upwards.

*Note - this calculation assumes the pump inlet is not pressurized and that friction losses are minimal. If the pump experiences a non-zero suction pressure, or if there is significant friction caused by the distance or material of the pipe, these should be factored in as well.

You"ll notice that the elevation head is minimal compared to the discharge pressure, and has minimal effect on the efficiency of the pump. As the elevation change increases or the discharge pressure decreases, however, elevation change will have a greater impact on total head.

Obviously, that’s a fair amount of math to get at the pump efficiency, considering all of the units conversions that need to be done. To avoid doing these calculations manually, feel free to use our simple pump efficiency calculator.

Our calculations use static variables (pump-rated horsepower and water source elevation) and dynamic variables (discharge flow and pressure). To determine pump efficiency, we need to measure the static variables only once, unless they change.

If you want to measure the true efficiency of your pump, taking energy consumption into account, you could add an electrical meter. Your meter should consist of a current transducer and voltage monitor (if using DC) for electrical motors or a fuel gauge for combustion. This would give you a true understanding of how pump efficiency affects energy consumption, and ultimately your bank account.

Up until this point, we’ve covered the ins and outs of how to determine pump efficiency. We’re now ready for the exciting stuff - how to improve pump efficiency!

One of the easiest ways to improve pump efficiency is to actually monitor pumps for signs of efficiency loss! If you monitor flow rate and discharge (output power) along with motor current or fuel consumption, you’ll notice efficiency losses as soon as they occur. Simply having pump efficiency information on hand empowers you to take action.

Another way to increase efficiency is to keep pumps well-maintained. Efficiency losses mostly come from mechanical defects in pumps, e.g., friction, leakages, and component failures. You can mitigate these issues through regular maintenance that keeps parts in working order and reveals impending failures. Of course, if you are continuously monitoring your pumps for efficiency drops, you’ll know exactly when maintenance is due.

You can also improve pump efficiency by keeping pumps lubricated at all times. Lubrication is the enemy of friction, which is the enemy of efficiency (“the enemy of my enemy is my friend…”).

A fourth way to enhance pump efficiency is to ensure your pumps and piping are sized properly for your infrastructure. Although we’re bringing this up last, it’s really the first step in any pumping operation. If your pumps and piping don’t match, no amount of lubricant or maintenance will help.

In this post, we’ve given you the full rundown when it comes to calculating and improving pump efficiency. You can now calculate, measure, and improve pump efficiency, potentially saving your business thousands of dollars annually on energy costs.

For those just getting started with pump optimization, we offer purpose-built, prepackaged solutions that will have you monitoring pump efficiency in minutes, even in hazardous environments.

The motor used to power a centrifugal pump needs to be able to produce enough torque to start the pump and bring it to an optimal operating speed. If a motor lacks enough torque to operate a pump, the pump may not start or may only operate at a reduced speed. The centrifugal pump suppliers at PumpWorks will guide you through the pump motor selection process.

A pump’s torque-speed curve is used to determine the appropriate motor to match with it. A pump’s torque-speed curve is produced by plotting the percentage of full load torque (FLT) vertically against the percentage of full load speed (FLS) plotted horizontally. An example is shown below.

The torque-speed curve is similar for all centrifugal pumps due to simple math: the pump torque varies as the square of its speed. However, when the pump is at rest—0% full load speed—the full load torque is never also 0%. Starting a rotating pump requires the motor to overcome the pump inertia and static friction.

To overcome pump inertia and static friction, approximately 20% of full load torque is required. As the pump’s speed increases, the required torque gradually declines. For example, at about 15% full load speed the required torque typically is around 5% or 10% full load torque. As shown below, the pump torque-speed curve follows the square law:

Like pumps, motors produce a torque-speed curve of their own. By overlaying the torque-speed curve of a pump and a motor, one can verify that the motor is producing enough accelerating torque to drive the pump to full speed, as shown below.

In this overlay the shaded area reflects the accelerating torque available from the motor to drive the pump. Where the two curves intersect is the point at which the motor’s torque is insufficient to drive the pump any faster. In other words, this is the point of maximum pump speed while powered by this motor.

A motor’s horsepower (HP) is used as a baseline measure of its capabilities in the field. HP is a combination of torque and speed (RPM), with 1 HP equal to 550 foot pounds per second, or 33,000 foot pounds per minute. A motor’s torque can be calculated using its horsepower using this formula, which is derived from an expression of HP as a function of torque:

Torque at zero flow is especially important for pumps with axial flow (or propeller) designs. The torque-speed curve of such pumps is such that the highest HP, and therefore the highest torque, is required at zero flow. An axial-flow pump must be paired with a motor with adequate HP to get the pump moving.

Another important factor in motor selection is the pump’s inertia value at the motor shaft. Inertia is a measure of an object’s resistance to movement change. The higher the pump inertia, the longer the motor will take to start the pump and bring it to full load speed.

This is significant because motors draw current to bring pumps up to speed. The longer a motor takes to overcome a pump’s inertia, the more heat it will generate. A motor must be sized to handle the pump’s inertia to avoid damaging the motor’s windings.

If a motor directly drives the pump, the values of the pump and pump-motor coupling inertias are the same regardless of pump speed.  If the pump is driven by a gearbox and motor, however, the gearbox can have a major impact on inertia values. In this application inertia can be expressed as:

A gearbox’s effect on inertia can be understood by analogy to a bicycle. When a bicycle is ridden at high speeds, the rider may change to a higher gear ratio (one greater than 1.0) to go faster. Such a ratio also requires the rider to put in more effort. Likewise, if a gearbox shifts to a higher gear ratio, the motor will have a higher load. The same logic applies if the gearbox is reducing the motor speed to drive the pump slower. When the gearbox ratio is less than 1.0, it will reduce the load requirements on the motor.

Selecting the right pump and motor for a specific application can be a complex job. The team at PumpWorks is dedicated to finding pump solutions that meet the exact needs of each customer.

In this article discussed about pump basic formulas with examples likepump power calculation formula, specific speed of centrifugal pump and affinity laws for centrifugal and displacement pumps. Also provided online calculator for pump power calculation

The work performed by the pump is equal to the weight of liquid pumped in Unit time multiplied by total Head in meters. However the pump capacity in M3/hr and liquid specific gravity are used rather than weight of liquid pumped for work done by the pump.

The input power “P” of a pump is the mechanical power inkW or Watt taken by the shaft or coupling. So the input power of the pump also called Break Horse Power (BHP).

Pump output power is called as Water Horse Power (WHP ) or Hydraulic power and it is useful work delivered by the pump.  and is usually expressed by the formula

The specific speed “Nq” is a parameter derived from a dimensional analysis which allows a comparison of impellers of various pump sizes even when their operating similar Q -H range.  The specific speed can be used to classify the optimum impeller design.

Specific Speed of pump (Nq) is defined as the speed in RPM at which a geometrically similar impeller would run if it were reduced proportionately in size so as to delivered 75 kg of water per second to the height of 1 m.

Pump Efficiency is the most important factor while calculating power consumption. So while selection of the higher rating of pump always choose best efficiency pump set.