wire rope breaking strength calculation price

Wire rope is also known by many other names, such as: wire, multi-strand wire, flexible wire, cable, cord, steelcord, etc. but it is essentially a collection of small filaments wound around each other in a manner that largely retains its shape when bent, crushed and/or tensioned.

It is a system for significantly increasing the strength and flexibility of steel wire and is used in almost every important application we see around us. For example: suspension bridges, tyres, brake and accelerator cables (in cars), high-pressure flexible pipes, lifting and rigging cables, electrical conductors, etc. and it comes in many different forms. Fig 2 shows just a very small sample of available designs.

With minor variations, the generally accepted method for designating a wire rope construction in the industry is by describing it numerically. For example:

Whilst "IWRC" wire ropes offer a slightly greater tensile capacity (≈7%) than those with fabric or polymer fillers, the additional strength does not come from the tensile capacity of the core filaments but from improved dimensional stability under load. And whilst they are also much more resistant to crushing, they are stiffer than fibre core ropes and therefore not recommended for applications where tension occurs under bending.

Warrington (Fig 1) is a parallel lay construction with an outer layer comprising wires of alternating large and small diameters, each outer layer having twice the number of wires as the layer immediately beneath. The benefit of this design is to increase packing and therefore strength density, however, unless the different diameter filaments are of the same strength (unlikely), this construction is limited by the strength of the weakest filaments.

Seale (Figs 1 & 2 6x36) is also a parallel lay construction but with the same number of wires in each wire layer. All the wires in any layer are the same diameter. This is an alternative to the Warrington construction, with similar benefits and disadvantages.

Regular lay constructions are used much more widely (than Lang lay) because they have excellent structural stability and less tendency to unwrap under tension (see Rotating vs Non-Rotating below). However, because it has a knobbly (undulating) surface it will wear both itself and any surface over which it is run much more quickly than Lang lay wire rope.

Lang lay constructions have a flatter surface than regular lay constructions giving them better resistance to wear and bending fatigue, especially when made from flattened (elliptical) filaments. They are, however, much less structurally stable and subject to birdcaging if the wire rope is over-bent or twisted against its wrapped direction.

"Regular Lay", multi-strand constructions are normally subject to slightly less rotation under tension (than Lang lay) due to the opposite helical direction of the filaments (within the strands) and the strands (within the rope), however, you can improve their rotation characteristics still further by;

Fillers (Fig 2) may be fabric, polymer or even smaller diameter filaments (e.g. 6x36). Whilst they contribute little to the tensile strength of wire rope, they can significantly; improve performance under bending (fabric and polymer cores only), reduce axial growth, reduce rotation in rotation-resistant constructions, improve structural stability and increase fatigue life.

This filler material should not be included in strength (tensile capacity) calculations, but must be included in those for axial stiffness (extension). If it is ignored, your calculations will reveal excessive extension as the wire rope collapses.

Suspension bridges tend to be constructed from densely packed, single strand plain "Wire Rope" constructions using large diameter galvanised filaments. Little heed is paid to rotational resistance as strength is paramount and once tensioned, they should remain in that loading condition for their design life.

Lifting & winching normally require wire ropes of good flexibility and fatigue resistance. Therefore they tend to be similar to 6x36 but with fibre core instead of the IWRC in Fig 2

Hosecord is suitable for HPHT flexible pipes as lateral flexibility is generally considered less important than minimal longitudinal growth or maximum tensile strength (per unit cross-sectional area).

Remote operating cables such as hand-brakes and accelerators on cars normally only work in tension so they need to be strong but not necessarily stiff (as they are fully contained in reinforced outer sheaths). These tend to be manufactured from large diameter "TyreCord" or small diameter single-strand "Wire Rope".

Wire rope does not obey Hooke"s law. Therefore, you cannot accurately predict how much it will stretch for any specified force. This unpredictability applies to any section removed from the same manufactured length of cord and even between cords produced to the same specification but by different manufacturers.

CalQlata has decided that the accuracy of axial stiffness (EA) of wire rope falls outside its own levels of acceptability and therefore does not include it in the wire rope calculator. The extension calculated in the Wire Rope calculator (δLᵀ) is based upon the effect of axial tension on packing density. It is therefore important that core material is not ignored when using the calculator to evaluate this characteristic.

Wire rope does not obey Hooke"s law. Therefore, you cannot accurately predict how much it will twist for any specified torque. This unpredictability applies to any section removed from the same manufactured length of cord and even between cords produced to the same specification but by different manufacturers.

CalQlata has decided that the accuracy of torsional stiffness (GJ) of wire rope falls outside its own levels of acceptability and therefore does not include it in the wire rope calculator.

1) No wire rope calculator, whether dedicated or generic, will accurately predict the properties of any single construction under a wide range of loading conditions

2) No wire rope calculator, whether dedicated or generic, will accurately predict any single property for a range of constructions under a wide range of loading conditions

The only wire rope that can be reliably analysed is that which is used for suspension bridges, because; it comprises a single strand, is very densely packed, has negligible twist, contains filaments of only one diameter, is never subjected to minimum bending and every filament is individually tensioned.

There is a very good reason why manufacturers do not present calculated performance data for construction or design proposals, because even they cannot accurately predict such properties and quite rightly rely on, and publish, test data.

During his time working in the industry, the wire rope calculator"s creator has seen, created and abandoned numerous mathematical models both simple and complex. He has gradually developed his own simplified calculation principle based upon his own experience that still provides him with consistently reliable results of reasonable accuracy.

The purpose of CalQlata"s wire rope calculator is to provide its user with the ability to obtain a reasonable approximation for a generic construction, after which, accurate test data should be sought from the manufacturer for the user"s preferred construction.

The calculation principle in the wire rope calculator is based upon changes in the properties of the wire rope that occur with variations in packing density under tension

Bearing in mind the above limitations CalQlata can provide the following assistance when generating (manipulating) the wire rope calculator"s input data and interpreting its output

Alternatively, for wire rope with multiple filament diameters, you need to find an equivalent diameter with the following proviso; you must enter the minimum filament yield stress (SMYS)

It is expected that apart from fillers, all the material in the wire rope will be identical and therefore have the same density, i.e. using different materials will result in less than "best" performance. However, if such a construction is proposed, you can calculate an equivalent density as follows:

It is expected that apart from fillers, all the material in the wire rope will be identical and therefore have the same tensile modulus, i.e. using different materials will result in less than "best" performance. However, if such a construction is proposed, you should enter the highest tensile modulus.

The wire rope calculator simply adds together the total area of all the filaments and multiplies them by the SMYS entered, which represents a theoretical maximum breaking load that would exist if this load is equally shared across all of the filaments and the lay angles have been arranged to eliminate localised (point) loads between adjacent filaments.

If the wire rope has been properly constructed it is likely that its actual break load will be greater than 80% of this theoretical value. However, given the vagaries of wire rope construction, the actual break load can vary considerably dependent upon a number of factors. CalQlata suggest that the following factors may be used to define the anticipated break load of any given construction:

The axial stiffness and strain under load will be affected by this value, hence the reason why the most reliable (predictable) constructions tend to be minimum [number of] strands and single filament diameter. The Warrington and Seale constructions and combinations thereof tend to provide the highest packing density (but lowest flexibility) and there is little to be gained from using these constructions in more than single stranded wire rope as the benefit of high-packing density will be lost with no gain in flexibility.

The anticipated second moment of area of the wire rope at tension "T" due to deformation but insignificant flattening as it is assumed the wire rope will be bent over a formed (shaped) sheave or roller.

The anticipated tensile modulus of the wire rope at tension "T" due to deformation but insignificant flattening as it is assumed the wire rope will be bent over a formed (shaped) sheave or roller.

It is not advisable to induce this bend radius in operation due to uncertainties associated with wire rope construction, especially for dynamic applications. CalQlata suggests that a similar approach to that used for the break load (Fb) above also be applied here, i.e.:

A change in diameter will occur in all wire rope, irrespective of construction, until packing density has reached a limiting value. The value provided in the wire rope calculator is that which would be expected if the construction remains intact at the applied tension "T"

Unreliability of this value increases with complexity in wire rope due to its longitudinal variability and the increased likelihood of premature failure.

The accuracy of this data will range from about ±1% for wire rope with a single strand and a single filament diameter, up to about ±15% for constructions of similar complexity to OTR cord

A change in length of any wire rope will occur due to the fact that the packing density increases with tension. This is not, however, a linear relationship.

This can be an unreliable value as illustrated by tests carried out (by the author) on two pieces of wire rope supplied by the same well-known manufacturer both of which were cut from the same length, varied in tensile capacity by only 1.5%, but the tensile modulus (and strain at break) varied by 34%. Whilst this was an extreme case, significant variations have been seen in wire rope manufactured by a number of manufacturers.

Whilst the wire rope calculator does not calculate axial stiffness (see Calculation Limitations 9) above), CalQlata can suggest the following rule-of-thumb that will provide reasonable results for most constructions at the applied tension "T":

Whilst the wire rope calculator does not calculate bending stiffness (see Calculation Limitations 8) above), CalQlata can suggest the following rule-of-thumb that will provide reasonable results for most constructions at the applied tension "T":

Low complexity means single strand and single wire diameter. Medium complexity means multi-strand and single wire diameter. High complexity means multi-strand and multiple wire diameters.

Rope strength is a misunderstood metric. One boater will talk about tensile strength, while the other will talk about working load. Both of these are important measurements, and it’s worth learning how to measure and understand them. Each of these measurements has different uses, and here we’re going to give a brief overview of what’s what. Here’s all you need to know about rope strength.

Each type of line, natural fiber, synthetic and wire rope, have different breaking strengths and safe working loads. Natural breaking strength of manila line is the standard against which other lines are compared. Synthetic lines have been assigned “comparison factors” against which they are compared to manila line. The basic breaking strength factor for manila line is found by multiplying the square of the circumference of the line by 900 lbs.

As an example, if you had a piece of ½” manila line and wanted to find the breaking strength, you would first calculate the circumference. (.5 X 3.14 = 1.57) Then using the formula above:

To calculate the breaking strength of synthetic lines you need to add one more factor. As mentioned above, a comparison factor has been developed to compare the breaking strength of synthetics over manila. Since synthetics are stronger than manila an additional multiplication step is added to the formula above.

Using the example above, letÂ’s find the breaking strength of a piece of ½” nylon line. First, convert the diameter to the circumference as we did above and then write the formula including the extra comparison factor step.

Knots and splices will reduce the breaking strength of a line by as much as 50 to 60 percent. The weakest point in the line is the knot or slice. However, a splice is stronger than a knot.

Just being able to calculate breaking strength doesn’t give one a safety margin. The breaking strength formula was developed on the average breaking strength of a new line under laboratory conditions. Without straining the line until it parts, you don’t know if that particular piece of line was above average or below average. For more information, we have discussed the safe working load of ropes made of different materials in this article here.

It’s very important to understand the fundamental differences between the tensile strength of a rope, and a rope’s working load. Both terms refer to rope strength but they’re not the same measurement.

A rope’s tensile strength is the measure of a brand-new rope’s breaking point tested under strict laboratory-controlled conditions. These tests are done by incrementally increasing the load that a rope is expected to carry, until the rope breaks. Rather than adding weight to a line, the test is performed by wrapping the rope around two capstans that slowly turn the rope, adding increasing tension until the rope fails. This test will be repeated on numerous ropes, and an average will be taken. Note that all of these tests will use the ASTM test method D-6268.

The average number will be quoted as the rope’s tensile strength. However, a manufacturer may also test a rope’s minimum tensile strength. This number is often used instead. A rope’s minimum tensile strength is calculated in the same way, but it takes the average strength rating and reduces it by 20%.

A rope’s working load is a different measurement altogether. It’s determined by taking the tensile strength rating and dividing it accordingly, making a figure that’s more in-line with an appropriate maximum load, taking factors such as construction, weave, and rope longevity into the mix as well. A large number of variables will determine the maximum working load of a rope, including the age and condition of the rope too. It’s a complicated equation (as demonstrated above) and if math isn’t your strong point, it’s best left to professionals.

However, if you want to make an educated guess at the recommended working load of a rope, it usually falls between 15% and 25% of the line’s tensile strength rating. It’s a lotlower than you’d think. There are some exceptions, and different construction methods yield different results. For example, a Nylon rope braided with certain fibers may have a stronger working load than a rope twisted out of natural fibers.

For safety purposes, always refer to the information issued by your rope’s manufacturer, and pay close attention to the working load and don’t exceed it. Safety first! Always.

If you’re a regular sailor, climber, or arborist, or just have a keen interest in knot-tying, be warned! Every knot that you tie will reduce your rope’s overall tensile strength. Some knots aren’t particularly damaging, while others can be devastating. A good rule of thumb is to accept the fact that a tied knot will reduce your rope’s tensile strength by around 50%. That’s an extreme figure, sure, but when it comes to hauling critical loads, why take chances?

Knots are unavoidable: they’re useful, practical, and strong. Splices are the same. They both degrade a rope’s strength. They do this because a slight distortion of a rope will cause certain parts of the rope (namely the outer strands) to carry more weight than others (the inner strand). In some cases, the outer strands end up carrying all the weight while the inner strands carry none of it! This isn’t ideal, as you can imagine.

Some knots cause certain fibers to become compressed, and others stretched. When combined together, all of these issues can have a substantial effect on a rope’s ability to carry loads.

Naturally, it’s not always as drastic as strength loss of 50% or more. Some knots aren’t that damaging, some loads aren’t significant enough to cause stress, and some rope materials, such as polypropylene, Dyneema, and other modern fibers, are more resilient than others. Just keep in mind that any knots or splices will reduce your rope’s operations life span. And that’s before we talk about other factors such as the weather or your rope care regime…

It is because of the versatility of wire rope that engineers must be deeply educated on tensile strength, as well as the impact that wire rope diameter and strand constructions can have on tensile strength, along with other critical characteristics such as cycle count and flexibility.

All wire ropes are tested for breaking strength. Motion cables have a minimum breaking strength requirement, which is determined by the material, diameter and construction of the wire rope. At Carl Stahl Sava Industries, wire rope is tested on tensile strength equipment. Either or both the wire rope itself can be tested against the minimum load requirement, or the fittings swaged to the wire rope can be similarly tested for their holding strength on the cable.

To ensure wire rope stays within its specified tensile limits, engineers will derate the minimum cable tensile strength by a safety factor. This is how engineers arrive at what is known as the Working Load Limit or WLL. The WLL safety factor of each cable being tested is application specific, but often times a factor of 3 to 5 is utilized. Divide the minimum tensile strength by the safety factor to calculate the safe working load limit for a specific cable.

Steel cables are made more durable in part due to a manufacturing process known as cold working or cold forming, where the material is shaped below its recrystallization temperature. Cold worked steel distorts the steel’s crystal grains in the flow of the metal, resulting in hardening of the material, thus strengthening it. Due to steel’s natural strength, combined with its well-known resistance to corrosion, engineers turn to steel cables for applications where exposure to harsh environments does not compromise wire rope integrity.

Although commonly mistaken for stranded cable, braided cable refers to the braided wrapping or insulation found in conductive cables, such as those transmitting power or data. This braided “jacket” insulates and strengthens the conductive, data or electric cable, making it more tolerant to time in the field, along with the twisting, turning and rolling to which braided cable is commonly exposed. Sava does not manufacture braided cable or other conductive cable, like coaxial and network cable, as none of these cables, commonly braided in nature, actuate motion.

Interestingly, even Google machine learning algorithms struggle to understand the differences between motion cable, such as steel wire rope or tungsten mechanical cable, and cables that transmit electricity or information. When a searcher uses Google or other common search engines like Bing or Yahoo! to find steel cable manufacturers like Sava, or for that matter, a maker of braided cable, the search engine confuses the two and often serves the wrong cable to the searcher.

Wire rope manufacturers offer a wide range of what is known as “cable constructions,” which characterizes the number of individual wires used to stranded the wire rope. Consequently, most wire rope comprises a center or “core” wire, that is then wrapped in more wires, thus completing the stand’s construction. In the case of a 1x7 steel cable construction, the core wire represents wire #1, wrapped in six additional wires. Hence 1x7 steel cable.

In many cases, that same 1x7 steel cable is then used as the core in the manufacture of larger, stronger and more durable steel cable. For instance, 7x19 steel cable strand comprises the original seven wires, or 1x7 strand, and is wrapped in 12 more wires, thus making a 7x19 construction. Said another way, the 7x19 wire rope consists of the original 1x7 strand, plus 12 additional wires, making for a total of 19 wires.

Less seldom are wire rope constructions that do not include a core wire. In these cases, take 3x7 cable construction for instance, three, 1x7 stranded wire ropes are wrapped around one another, forming a triangular-shaped wire rope construction.

Wire ropes are largely used in marine environment or for rigging purposes. They receive considerable loads and thus suffer a great deal of mechanical damage throughout their service life. Moreover, research has shown that the major cause of wire rope failure is excessive deterioration and corrosion, lack of maintenance and inspection, and wrong usage resulting in early discarding, reduced safety and replacement cost increase.

Sometimes damage can be easily detected, while in other cases fractured wires may occur on the inside. Hence, wire ropes should be inspected and maintained by the right person (competent person assigned by the company), to assure they’re in perfect condition. Regular inspectionsensure high rope performance, long service lifetime , safety of personnel and equipment, and reduced operating costs.

All ropes (synthetic, high modulus and wire ropes) should be inspected before and after an operation. This guideline ensures maximum safety for both a ship’s personnel and equipment. Even though it’s difficult to determine the exact service life span of ropes, there is a way to have a more precise estimation about their efficient lifecycle. Calculating the exact time ropes have been in use (e.g mooring time, mooring conditions, weather and tidal conditions) is the answer. All in all, rope inspections should occur at least once a year.

Inspecting wire ropes in particular, comes with great responsibility. Inspection results should be recorded, and any defects noticed have to be reported and addressed properly. Some defects can be repaired, while in some cases replacing a wire rope is inevitable.

Periodical inspections ofvessel deck equipment is also crucial for maintaining the good condition of wire ropes. The condition of the drum, chocks, bitts, rollers, sheaves, cable clamps and other end fittings, affect the rope’s performance, threads and cords. Make sure to mark these parts during your overall inspection.

In order to help marine officers and staff conduct successful wire rope inspections – and keep an up-to-date record of them – we have created an inspection solution that helps in maintaining and monitoring a ship’s ropes and deck equipment.Learn more about Katradis inspection Neptune Solution

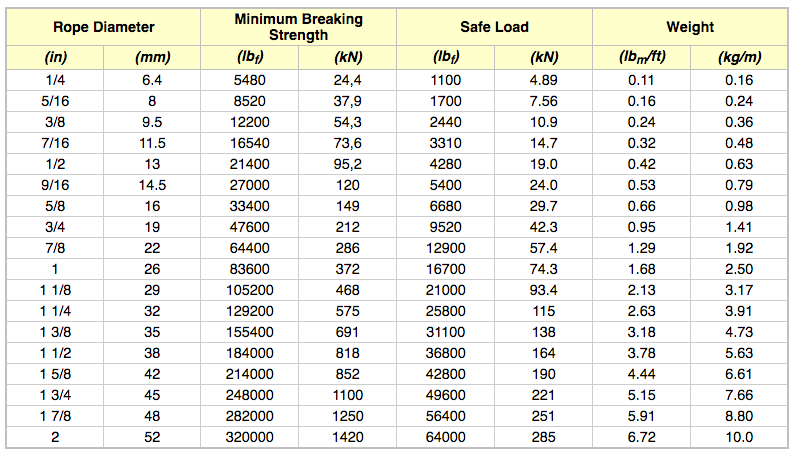
When calculating mass using F = Minimum Breaking Force, according to the wire rope’s diameter, you can determine the Minimum Breaking Massand therefore the wire’s max strength. When calculating mass using F = Safe Load according to the wire rope’s diameter, you can determine the Safe Load Mass,which is the advised load for this rope diameter.

The strands of a wire rope absorb the majority of the tensile force applied on the rope. Their design and manufacturing standards affect the level of fatigue resistance and resistance to abrasion. An easy way to understand which rope design is suitable for each purpose, is the wire rope classification.

Wire ropes are classified according to the number of strands in each construction and the number of wires in each strand. For example, a classification of 6X19 means that a wire rope of this type always has six strands, but its wires could be 15-26 per strand. This is because 19 is not the exact number of wires, but the classification of a wire number range.

Visual inspections are a common and fast way to assess wire rope condition. Both the standard and rotation resistant wire rope inspectionprocesscomply with the same four steps of examination. A ship’s crew can perform them as follows:

Steel wire rope distortion is obvious in most cases and can easily be identified by the inspector or the ship‘s crew. It usually occurs if load is suddenly applied or abruptly released (shock loading), or even if swift torque is forcefully induced.

Although not all of these deformations make the rope absolutely dangerous to use, they all may cause ropes to wear unevenly in time. This means inspections should take place more often, and distorted ropes should be handled with caution.

The rag and visual inspection is a good method for regular inspection intervals. The inspector pulls a rag along the rope trying to find broken wire cords. If the rug gets snagged by the rope, the inspector has to stop and assess the wire rope’s condition. Extreme caution should be exercised during the visual inspection, and under no circumstances should this method be the only one used to inspect wire ropes.

Tip: When you encounter a protruding wire end, bend it back and forth manually, until it separates from the wire. This will protect neighboring wires from wearing out.

Diameter reduction is a critical factor in steel wire rope wear and if not properly taken care of, it can result in rope breakage. Excessive abrasion, loss of core mass, corrosion or inner wire failure are all factors that contribute to diameter reduction.

To get an accurate measurement of the rope’s diameter, measure the rope at three different points at least 5 feet apart. Take the average of these three measurements to determine the true diameter.

Any measurements showing a reduction of ⅓ or more, indicate that a replacement should follow without delay. A diameter reduction of less than 1/3 still requires attention, and the inspector or the ship’s crew should be on guard in the next scheduled wire rope inspection.

Failure from abrasion or corrosion is a result of deficient deck equipment inspection or insufficient wire rope lubrication respectively. Internal corrosive damage is more difficult to identify than any other types of degradation. In most cases, the damage has progressed more than the external signs suggest.

Wire rope storage plays a significant role in the rope’s operation life.Wire rope corrosion and pitting can be avoided if ropes are safely stored in a clean, cool, dry and well-ventilated place. Steel wire ropes should not by any means rest on the floor, and should be protected from water, dust or any chemical fumes. Long term storage requires periodic greasing, turning the reel upside down for preventing grease dripping and possibly re-winding to another reel with larger inner tube diameter.

Wire ropes should be maintained with periodical lubrication. In order to prevent internal corrosion, a pressure lubricator is suggested to be used. In this case, a small amount of grease is used to lubricate the rope internally, while the deck stays grease-clean. Pressure lubricators clean the rope before they grease it so that the new grease enters a clean rope. The type of grease used is very important for maximum protection and greasing efficiency.

Steel wire ropes exposed to dirt, grime and other contaminants, have to be cleaned with a wire brush and petroleum (unless a pressure lubricator is used). Optimal cleaning of wire ropes can extend their service life and guarantee safe operations.

The reeling process is of high importance for the longevity of wire ropes. To protect them from being damaged, it is important that the surface of the drum is clean, smooth and dry. Improper reeling may cause wire-rope strands to spread or get flattened, when in contact with one another, as successive layers are being spooled and upper layers apply pressure on the lower ones.

Katradis S.A. offers a wide range of top quality wire ropes for shipping (mooring and hoisting operations), fishing and construction purposes. Our wire ropes have greater resistance to fatigue, and they distribute tension force equally among the rope strands. They are less likely to kink, providing higher staff safety and assuring operation success.Choose your new wire ropes

Ropes made from high modulus polyethylene (HMPE) have superior tension fatigue properties compared to ropes made from steel wire or other synthetic fibers (i.e. nylon, polyester, aramids, etc.), as shown in Table 1.

The testing summarized in this document is focused on HMPE-based ropes. The test included two samples of each rope type from three different manufactures, referred to here as AmSteel®-Blue and Saturn-12 (both Samson products), Product C, and Product D (from 2 different domestic manufacturers). All samples were 12-strand single braids, 3/8” (9 mm) nominal diameter, made from HMPE fiber (Samson AmSteel®-Blue and Saturn-12 are 100% Dyneema® HMPE fiber, Product C and D are 100% Spectra® HMPE fiber). Product D uses heat setting in post processing while Product C uses construction design characteristics that optimize break strength and keep stretch low. Samson’s two products use a balanced construction that strives to achieve high strength and low stretch while maximizing fatigue life and abrasion resistance.

The effects of heat setting on HMPE rope is well documented (see Samson Technical Bulletin: HMPE Rope—Effects of Post Production Processes). HMPE ropes characteristically show an initial increase in strength as they are worked for the first 40% of their expected tension fatigue lifetime. Heat setting pushes the rope along the expected strength curve to the maximum strength the fiber will be expected to achieve before it is placed in service. The strength gain comes at the price of a significantly reduced fatigue lifetime.

The rope’s construction design—twist levels and braid angles—also influences both strength, fatigue life and resistance to abrasion. (See Samson Technical Bulletin: HMPE Rope: Design vs. Performance). High strength can be achieved using a longer cycle length that results in a looser braid. Testing shows that it also results in lower tension fatigue resistance and lower abrasion resistance

Typically the diameter of halyards and sheets is determined by clutches, cleats and blocks on board of your ship. If you are into yacht racing or rigging a new boat, it can be good to calculate the minimum required breaking load of sheets and halyards in order to reduce weight of ropes onboard. Calculating the required breaking load is a more precise approach for determining the diameter of sheets and halyards.

It is a good idea to build in some safety margin in your calculations. Often a safety factor of 4 is used, which means that a rope will receive a workload of only 25% of the breaking load. This is so called Safe Working Load. In practice, however, sails are usually reefed or the boat is in a safe harbour before a rope is loaded to its maximum. That is why we use a safety ratio for cruising yachts of 2 and even 1.5 for racing yachts.

Bear in mind that the weakest link counts. A splice typically reduces the strength by 5-10% but a knot can take off 50% of the strength. For these calculations we assume that the ropes will be spliced.

For halyards and genoa sheets you can easily calculate the breaking strength by multiplying your sheet size in square meters with 30 (for spinnakers take 13). This allows you to handle your sails still at 7 Bft  (41-47knots). We have done the maths for you in the table below. Loads can vary slightly for e.g. catamaran, but variations are usually covered by the safety factor.

For halyards with a 1:2 purchase, you can divide the breaking strength by two. Please note that clutches, cleats, blocks and shackles still bear the full load though!

For mainsheets one important factor needs to be added to the calculations: being the point where the main sheet is attached to the boom. This then results in the formula below with these factors:

The calculated breaking strength of a steel wire rope is defined as the metallic cross section of a steel wire rope (the sum of the individual cross sections of all the wires making up the rope) multiplied by the nominal tensile strength of the steel wire rope. The minimum breaking strength of the steel wire rope is the calculated breaking strength of the rope multiplied by the spin factor.

The actual breaking strength of a steel wire rope is the breaking strength of the rope as determined in a pull test. A new steel wire rope must achieve an actual breaking strength equal to or higher than the minimum breaking strength. The breaking strength of a steel wire rope can be increased by increasing the metallic area of the rope (e.g. by using strands with higher fill factors, by compacting the strands or by swaging the rope), by increasing the tensile strengths of the individual wires or by increasing the spin factor of the rope. This can also be achieved by improving the contact conditions between the rope elements by using a plastic infill.

The bending fatigue resistance of steel wire ropes is defined as the number of bending cycles a rope can achieve in a bending fatigue test under defined parameters (e.g. running over sheaves with a defined diameter and a predetermined line pull corresponding to the MBL of the steel wire rope). The bending fatigue resistance of the steel wire rope increases with increasing D/d ratio (= sheave diameter (D): nominal rope diameter (d)) and by reducing the line pull. The bending fatigue resistance of a steel wire rope can be increased by increasing the contact area between the steel wire rope and the sheave and by increasing the contact conditions between the rope elements, by adding a plastic layer between the IWRC and the outer strands. Due to the larger contact area between the ropes and the sheaves and due to the increased flexibility, 8- strand ropes are more resistant to bending fatigue than 6- strand ropes of a similar design.

The flexibility of a steel wire rope typically increases with increasing a number of strands and wires in the rope. The flexibility is also influenced by the lay lengths of the strands, of the rope core and the rope as well as by the gaps between wires and strands. If a rope is not flexible enough, it will have to be forced to bend around a sheave of a given diameter, which will reduce the bending fatigue life of the rope. It will also be forced to bend around a drum of a given diameter. Spooling problems might be a consequence.

When running over a sheave a rope has to be converted from a straight condition into a bent condition at the point when the rope runs onto the sheave and has to be converted again from the bent into the straight condition when it runs off the sheave. Also the bearing has to be turned. In doing so, the friction forces in the rope as well as the friction forces in the bearing have to be overcome. This leads to a change of the rope force. One describes the relationship of the rope force on both sides of the sheave as the efficiency factor and accepts that this numerical value also takes into account the friction losses of the bearing. When measuring the efficiency factor of a rope the loss of the line pull while the rope is running over the sheave is measured. An efficiency factor of 0,98, or alternatively a strength loss of 2%, is generally assumed for wire ropes.