how to calculate mud pump efficiency made in china

This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data.

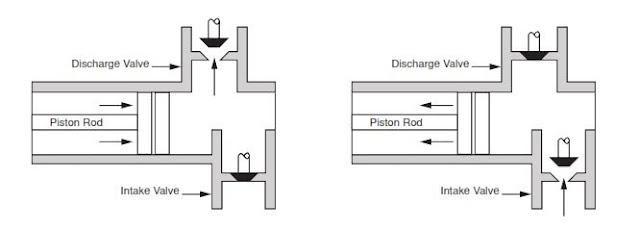
Rig pump output, normally in volume per stroke, of mud pumps on the rig is  one of important figures that we really need to know because we will use pump out put figures to calculate many parameters such as bottom up strokes,  wash out depth, tracking drilling fluid, etc. In this post, you will learn how to calculate pump out put for triplex pump and duplex pump in bothOilfield and Metric Unit.

This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data.

This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data.

This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data.

The mud pump piston is a key part for providing mud circulation, but its sealing performance often fails under complex working conditions, which shorten its service life. Inspired by the ring segment structure of earthworms, the bionic striped structure on surfaces of the mud pump piston (BW-160) was designed and machined, and the sealing performances of the bionic striped piston and the standard piston were tested on a sealing performance testing bench. It was found the bionic striped structure efficiently enhanced the sealing performance of the mud pump piston, while the stripe depth and the angle between the stripes and lateral of the piston both significantly affected the sealing performance. The structure with a stripe depth of 2 mm and angle of 90° showed the best sealing performance, which was 90.79% higher than the standard piston. The sealing mechanism showed the striped structure increased the breadth and area of contact sealing between the piston and the cylinder liner. Meanwhile, the striped structure significantly intercepted the early leaked liquid and led to the refluxing rotation of the leaked liquid at the striped structure, reducing the leakage rate.

Mud pumps are key facilities to compress low-pressure mud into high-pressure mud and are widely used in industrial manufacture, geological exploration, and energy power owing to their generality [1–4]. Mud pumps are the most important power machinery of the hydraulic pond-digging set during reclamation [5] and are major facilities to transport dense mud during river dredging [6]. During oil drilling, mud pumps are the core of the drilling liquid circulation system and the drilling facilities, as they transport the drilling wash fluids (e.g., mud and water) downhole to wash the drills and discharge the drilling liquids [7–9]. The key part of a mud pump that ensures mud circulation is the piston [10, 11]. However, the sealing of the piston will fail very easily under complex and harsh working conditions, and consequently, the abrasive mud easily enters the kinematic pair of the cylinder liner, abrading the piston surfaces and reducing its service life and drilling efficiency. Thus, it is necessary to improve the contact sealing performance of the mud pump piston.

As reported, nonsmooth surface structures can improve the mechanical sealing performance, while structures with radial labyrinth-like or honeycomb-like surfaces can effectively enhance the performance of gap sealing [12–14]. The use of nonsmooth structures into the cylinder liner friction pair of the engine piston can effectively prolong the service life and improve work efficiency of the cylinder liner [15–17]. The application of nonsmooth grooved structures into the plunger can improve the performance of the sealing parts [18, 19]. The nonsmooth structures and sizes considerably affect the sealing performance [20]. Machining a groove-shaped multilevel structure on the magnetic pole would intercept the magnetic fluid step-by-step and slow down the passing velocity, thus generating the sealing effect [21–23]. Sealed structures with two levels or above have also been confirmed to protect the sealing parts from hard damage [24]. The sealing performance of the high-pressure centrifugal pump can be improved by adding groove structures onto the joint mouth circumference [25]. The convex, pitted, and grooved structures of dung beetles, lizards, and shells are responsible for the high wear-resistance, resistance reduction, and sealing performance [26–28]. Earthworms are endowed by wavy nonsmooth surface structures with high resistance reduction and wear-resistance ability [29]. The movement of earthworms in the living environment is very similar to the working mode of the mud pump piston. The groove-shaped bionic piston was designed, and the effects of groove breadth and groove spacing on the endurance and wear-resistance of the piston were investigated [30]. Thus, in this study, based on the nonsmooth surface of earthworms, we designed and processed a nonsmooth striped structure on the surface of the mud pump piston and tested the sealing performance and mechanism. This study offers a novel method for prolonging the service life of the mud pump piston from the perspective of piston sealing performance.

The BW-160 mud pump with long-range flow and pressure, small volume, low weight, and long-service life was used here. The dimensions and parameters of its piston are shown in Figure 1.

A striped structure was designed and processed on the contact surface between the piston cup and the cylinder liner. The striped structure was 5 mm away from the outermost part of the lip, which ensured the lip could contact effectively with the cylinder liner. Based on the structural dimensions of the piston cup, we designed a 2-stripe structure, and the very little stripe space affected the service life of the piston [30]. Thus, the stripe space of our bionic piston was set at 5 mm. According to the machining technology, two parameters of stripe depth h and the angle between the stripes and lateral of the piston α were selected (Figure 2).

A mud pump piston sealing performance test bench was designed and built (Figure 3). This bench mainly consisted of a compaction part and a dynamic detection part. The compaction part was mainly functioned to exert pressure, which was recorded by a pressure gauge, to the piston sealed cavity. This part was designed based on a vertical compaction method: after the tested piston and the sealing liquid were installed, the compaction piston was pushed to the cavity by revolving the handle. Moreover, the dynamic detection part monitored the real-time sealing situation and was designed based on the pressure difference method for quantifying the sealing performance. This part was compacted in advance to the initial pressure P0 (0.1 MPa). After compaction, the driving motor was opened, and the tested piston was pushed to drive the testing mud to reciprocate slowly. After 1 hour of running, the pressure P on the gauge was read, and the pressure difference was calculated as , which was used to measure the sealing performance of the piston.

To more actually simulate the working conditions of the mud pump, we prepared a mud mixture of water, bentonite (in accordance with API Spec 13A: viscometer dial reading at 600 r/min ≥ 30, yield point/plastic viscosity radio ≤ 3, filtrate volume ≤ 15.0 ml, and residue of diameter greater than 75 μm (mass fraction) ≤ 4.0%), and quartz sand (diameter 0.3–0.5 mm) under complete stirring, and its density was 1.306 g/cm³ and contained 2.13% sand.

The orthogonal experimental design method was used to study the effect of factors and the best combination of factor levels [31]. Stripe depth h and angle α were selected as the factors and were both set at three levels in the sealing performance tests (Table 1).

The test index was the percentage of sealing performance improvement β calculated aswhere and are the pressure differences after the runs with the standard and the bionic pistons, respectively ().

The sealing performance tests showed the striped structures all effectively enhanced the contact sealing between the piston and the cylinder liner. In particular, the increase of sealing performance relative to the standard piston minimized to 21.05% in the bionic striped piston with a stripe depth of 3 mm and angle of 45° and maximized to 90.79% in the bionic striped piston with the stripe depth of 2 mm and angle of 90°. Range analysis showed the sealing performance of pistons was affected by the stripe depth h and angle α, and these two parameters (h and α) have the same effect on the sealing performance.

Figure 4 shows the effects of stripe depth and angle on the sealing performance of mud pump pistons. Clearly, the stripe depth should be never too shallow or deep, while a larger angle would increase the sealing performance more (Figure 4).

Sealing validity tests were conducted to validate the sealing performance of the bionic striped pistons. It was observed whether the sealing liquid would leak at the tail of the cylinder liner, and the time of leakage was recorded. The standard piston and the most effective bionic piston were selected to compare their sealing performances.

Both the standard piston and the bionic striped piston leaked, which occurred after 84 and 249 minutes of operation, respectively (Figure 5). Figure 6 shows the pressures of the two pistons during testing. Clearly, the sealing pressure of the standard piston declined rapidly before the leakage, but that of the bionic piston decreased very slowly. After the leakage, the reading on the pressure gauge in the standard piston declined to 0 MPa within very short time, but that of the bionic piston decreased much more slowly.

The beginning time of leakage was inconsistent between the standard and bionic pistons (84 minutes vs. 249 minutes). In order to compare the leakage of these two pistons, the leaked liquid was collected when the piston started to leak. The volume of the leaked liquid was measured using a graduated cylinder every 5 minutes from the 84th minute and 249th minute, respectively (both considered as 0 minute), for 20 minutes. Figure 7 shows the leaked amounts of the standard piston and the bionic piston. Clearly, after the leakage and failure, the leaking speed and amount of the bionic piston were both smaller than those of the standard piston.

The piston lips and the cylinder liner were under interference contact, and their mutual extrusion was responsible for the lip sealing. Thus, a larger pressure between the piston lips and the cylinder liner reflects a higher lip sealing effect.

The bionic striped piston with the highest sealing performance (h = 2 mm, α = 90°) was selected for the sealing mechanism analysis and named as the bionic piston. The 3D point cloud data of standard piston were acquired by using a three-dimensional laser scanning system (UNIscan, Creaform Inc., Canada). Then, the standard piston model was established by the reverse engineering technique. The striped structure of the bionic piston was modeled on basis of the standard piston.4.1.1. Contact Pressure of Piston Surface

The standard piston and the bionic piston were numerically simulated using the academic version of ANSYS® Workbench V17.0. Hexahedral mesh generation method was used to divide the grid, and the size of grids was set as 2.5 mm. The piston grid division is shown in Figure 8, and the grid nodes and elements are shown in Table 3. The piston cup was made of rubber, which was a hyperelastic material. A two-parameter Mooney–Rivlin model was selected, with C10 = 2.5 MPa, C01 = 0.625 MPa, D1 = 0.3 MPa−1, and density = 1120 kg/m3 [32, 33]. The loads and contact conditions related to the piston of the mud pump were set. The surface pressure of the piston cup was set as 1.5 MPa, and the displacement of the piston along the axial direction was set as 30 mm. The two end faces of the cylinder liner were set as “fixed support,” and the piston and cylinder liner were under the frictional interfacial contact, with the friction coefficient of 0.2.

Figure 9 shows the pressure clouds of the standard piston and the bionic piston. Since the simulation model was completely symmetrical and the pressures at the same position of each piston were almost the same, three nodes were selected at the lip edge of each piston for pressure measurement, and the average of three measurements was used as the lip edge pressure of each piston. The mutual extrusion between piston and cylinder liner happened at the lip, and thereby the larger of the lip pressure was, the better the sealing performance was. The lip pressure of the standard piston was smaller than that of the bionic piston (2.7371 ± 0.016 MPa vs. 3.0846 ± 0.0382 MPa), indicating the striped structure enhanced the mutual extrusion between the bionic piston and the cylinder liner and thereby improved the sealing performance between the lips and the cylinder liner. As a result, sand could not easily enter the piston-cylinder liner frictional interface, which reduced the reciprocated movement of sand and thereby avoided damage to the piston and the cylinder liner.

Figure 10 shows the surface pressures from the lip mouth to the root in the standard piston and the bionic piston. The surface pressure of the bionic piston surpasses that of the standard piston, and the pressure at the edge of each striped structure changes suddenly: the pressures at the striped structure of the bionic piston are far larger than at other parts. These results suggest the contact pressure between the edges of the striped structures and the cylinder liner is larger, and the four edges of the two striped structures are equivalent to a four-grade sealed lip mouth formed between the piston and the cylinder liner, which generates a multilevel sealing effect and thereby largely enhances the sealing effect of the piston.

The piston surface flow field was numerically simulated using the CFX module of the software ANSYS® Workbench V17.0. The side of the lips was set as fluid inlet, and the other side as fluid outlet, as shown in Figure 11. The inlet and outlet were set as opening models, and the external pressure difference between them was 0 Pa. The moving direction of the piston was opposite to the fluid flow direction. The fluid region was divided into grids of 0.2 mm, while the striped structures were refined to grade 2.

Figures 12 and 13 show the surface streamline clouds and sectional streamline clouds of the two pistons at the early stage of leakage when the fluid entered the interface. Clearly, compared with the standard piston, when the surface-leaked liquid from the bionic piston passed the striped structure, the streamlines were sparse and significantly decreased in number, and the flow velocity declined more. The flow velocity decreased from 0.9348 m/s to 0.7555 m/s in the bionic piston and from 0.9346 m/s to 0.9262 m/s in the standard piston. It shows that, after the blockage by the striped structures, the striped structure more significantly intercepted the leaked liquid and could reduce the leakage rate of the piston, thereby enhancing the sealing effect.

Figure 13 shows the section leakage streamline of the standard piston and the bionic piston. Clearly, compared with the standard piston, when the leaked liquid of the bionic piston flowed through the striped structures, the streamlines would reflux and reverse inside the striped structures, indicating the striped structures can efficiently store the leaked liquid and slow down the leakage.

To better validate the sealing mechanism of the bionic striped pistons, a piston’s performance testing platform was independently built and the sealed contact of the pistons was observed. A transparent toughened glass cylinder liner was designed and machined. The inner diameter and the assembly dimensions of the cylinder liner were set according to the standard BW-160 mud pump cylinder liners. The sealing contact surfaces of the pistons were observed and recorded using a video recorder camera.

Figure 14 shows the surface contact of the standard piston and the bionic piston. Clearly, in the contact areas between the standard piston and the cylinder liner, only the narrow zone at the lip mouth contacted, as the contact width was only 4.06 mm. On the contrary, the contact areas between the bionic piston and the cylinder liner were all very wide, as the contact width was about 18.36 mm, and the sealed area was largely enlarged (892.8 mm2 vs. 4037.6 mm2) according to the contact areas calculated, which were favorable for improving the sealing performance.

Figure 15 shows the oil film left after the piston running. The oil film width of the bionic piston was far larger than that of the standard piston (20.48 mm vs. 2.28 mm). The striped structure of the bionic piston could store the lubricating oils, and uniform oil films were formed after its repeated movement, which reduced the friction between the piston and the cylinder liner, so that the seal failure of the piston would not happen due to excessive abrasion.

(1)The bionic striped structure significantly enhanced the sealing performance of the mud pump pistons. The stripe depth and the angle between the stripes and the piston were two important factors affecting the sealing performance of the BW-160 mud pump pistons. The sealing performance was enhanced the most when the stripe depth was 2 mm and the angle was 90°.(2)The bionic striped structure can effectively enhance the contact pressure at the piston lips, enlarge the mutual extrusion between the piston and the cylinder liner, reduce the damage to the piston and cylinder liner caused by the repeated movement of sands, and alleviate the abrasion of abrasive grains between the piston and the cylinder liner, thereby largely improving the sealing performance.(3)The bionic striped structure significantly intercepted the leaked liquid, reduced the leakage rate of pistons, and effectively stored the leaked liquid, thereby reducing leakage and improving the sealing performance.(4)The bionic striped structure led to deformation of the piston, enlarged the width and area of the sealed contact, the stored lubricating oils, and formed uniform oil films after repeated movement, which improved the lubrication conditions and the sealing performance.

The bionic striped structure can improve the sealing performance and prolong the service life of pistons. We would study the pump resistance in order to investigate whether the bionic striped structure could decrease the wear of the piston surface.

Find W series mud pump from pressure grouting pump manufacturer - Saigao gruop in China. The W series mud pump can be widely used in all kinds of works in oil field, which is su...

Drilling consumables such as mud pump systems and their components can drastically increase your uptime while reducing costs and health/safety/environmental (HSE) risks. To support your drilling needs, Forum’s patented P-Quip® mud pump system offers a single-source solution that integrates high-quality fluid end components for maximum longevity and performance.

With more than 20 years of successful operation in severe environments, P-Quip offers a proven track record for the lowest cost of ownership in the industry. As part of our commitment to quality, our mud pump parts use patented Banded Bore™ technology that significantly reduces stress concentrations and leads to longer module life.

One of Forum’s most committed core values is that “no one gets hurt,” and the P-Quip system is designed to support that principle. Streamlined and easy to use, it reduces or eliminates the need for manual force during maintenance, shrinking the time needed to replace high-use components and minimizing safety risks.

If you are supplying pump supplies, you can find the most favorable prices at Alibaba.com. Whether you will be working with piston type or diaphragm type systems, reciprocating or centrifugal, Alibaba.com has everything you need. You can also shop for different sizes mud pump wholesale for your metering applications. If you operate a construction site, then you could need to find some concrete pump solutions that you can find at affordable rates at Alibaba.com. Visit the platform and browse through the collection of submersible and inline pump system, among other replaceable models.

A mud pump comes in different makes and sizes, and you buy the tool depending on the application. The pump used by a filling station is not the one you use to fill up your tanks. There are high flow rate low pressure systems used to transfer fluids axially. On the other hand, you can go with radial ones dealing with a low flow rate and high-pressure fluid. The mixed flow pump variety combines radial and axial transfer mechanisms and works with medium flow and pressure fluids. Depending on what it will be pumping, you can then choose the mud pump of choice from the collection at Alibaba.com.

Alibaba.com has been an excellent wholesale supplier of mud pump for years. The supply consists of a vast number of brands to choose from, comes in different sizes, operations, and power sources. You can get a pump for residential and large commercial applications from the collection. Whether you want a water pump for your home, or run a repair and maintenance business, and need a supply ofud pump, you can find the product you want from the vast collection at Alibaba.com.therther is refrigeration, air conditioning, transfer, or a simple car wash business, anything you want, Alibative.com can it you.

Pumps tend to be one of the biggest energy consumers in industrial operations. Pump motors, specifically, require a lot of energy. For instance, a 2500 HP triplex pump used for frac jobs can consume almost 2000 kW of power, meaning a full day of fracking can cost several thousand dollars in energy costs alone!

So, naturally, operators should want to maximize energy efficiency to get the most for their money. Even a 1% improvement in efficiency can decrease annual pumping costs by tens of thousands of dollars. The payoff is worth the effort. And if you want to remotely control your pumps, you want to keep efficiency in mind.

In this post, we’ll point you in the right direction and discuss all things related to pump efficiency. We’ll conclude with several tips for how you can maintain pumping efficiency and keep your energy costs down as much as possible.

In simple terms, pump efficiency refers to the ratio of power out to power in. It’s the mechanical power input at the pump shaft, measured in horsepower (HP), compared to the hydraulic power of the liquid output, also measured in HP. For instance, if a pump requires 1000 HP to operate and produces 800 HP of hydraulic power, it would have an efficiency of 80%.

Remember: pumps have to be driven by something, i.e., an electric or diesel motor. True pump system efficiency needs to factor in the efficiency of both the motor AND the pump.

Consequently, we need to think about how electrical power (when using electric motors) or heat power (when using combustion engines) converts into liquid power to really understand pump efficiency.

Good pump efficiency depends, of course, on pump type and size. High-quality pumps that are well-maintained can achieve efficiencies of 90% or higher, while smaller pumps tend to be less efficient. In general, if you take good care of your pumps, you should be able to achieve 70-90% pump efficiency.

Motor efficiency is also an important factor here. Motor efficiency depends on the fuel type, whether electricity or hydrocarbon, which in turn depends on availability and cost.

AC motors can achieve 90%+ efficiency when converting electrical to mechanical energy. Combustion engines are much less efficient, with typical efficiency ratings coming in at ~20% for gasoline and ~40% for diesel. Your choice of engine or motor type will depend on the availability and cost of fuel or electricity in your area.

Electric motors are more efficient than combustion engines, but site location and the cost of fuel can make the choice of combustion engines more practical.

Now that we have a better understanding of the pump efficiency metric, let’s talk about how to calculate it. The mechanical power of the pump, or the input power, is a property of the pump itself and will be documented during the pump setup. The output power, or hydraulic power, is calculated as the liquid flow rate multiplied by the "total head" of the system.

Remember: we’re trying to find the ratio of power in to power out. Since rations require equal units on both sides, we"ll have to do some conversions to get our hydraulic power units in HP. You"ll see how this is done in the example below.

IMPORTANT: to calculate true head, you also need to factor in the work the pump does to move fluid from the source. For example, if the source water is below the pump, you need to account for the extra work the pump puts in to draw source water upwards.

*Note - this calculation assumes the pump inlet is not pressurized and that friction losses are minimal. If the pump experiences a non-zero suction pressure, or if there is significant friction caused by the distance or material of the pipe, these should be factored in as well.

Every foot of water creates an additional 0.434 PSI of pressure, so we"ll find the elevation head by converting the change in elevation in feet to the suction pressure created by the water.

You"ll notice that the elevation head is minimal compared to the discharge pressure, and has minimal effect on the efficiency of the pump. As the elevation change increases or the discharge pressure decreases, however, elevation change will have a greater impact on total head.

Obviously, that’s a fair amount of math to get at the pump efficiency, considering all of the units conversions that need to be done. To avoid doing these calculations manually, feel free to use our simple pump efficiency calculator.

Our calculations use static variables (pump-rated horsepower and water source elevation) and dynamic variables (discharge flow and pressure). To determine pump efficiency, we need to measure the static variables only once, unless they change.

If you want to measure the true efficiency of your pump, taking energy consumption into account, you could add an electrical meter. Your meter should consist of a current transducer and voltage monitor (if using DC) for electrical motors or a fuel gauge for combustion. This would give you a true understanding of how pump efficiency affects energy consumption, and ultimately your bank account.

Up until this point, we’ve covered the ins and outs of how to determine pump efficiency. We’re now ready for the exciting stuff - how to improve pump efficiency!

One of the easiest ways to improve pump efficiency is to actually monitor pumps for signs of efficiency loss! If you monitor flow rate and discharge (output power) along with motor current or fuel consumption, you’ll notice efficiency losses as soon as they occur. Simply having pump efficiency information on hand empowers you to take action.

Another way to increase efficiency is to keep pumps well-maintained. Efficiency losses mostly come from mechanical defects in pumps, e.g., friction, leakages, and component failures. You can mitigate these issues through regular maintenance that keeps parts in working order and reveals impending failures. Of course, if you are continuously monitoring your pumps for efficiency drops, you’ll know exactly when maintenance is due.

You can also improve pump efficiency by keeping pumps lubricated at all times. Lubrication is the enemy of friction, which is the enemy of efficiency (“the enemy of my enemy is my friend…”).

The best way to ensure lubrication is to monitor lube tanks or sumps and make sure you always have lubrication on hand. You can also monitor lubricant consumption for significant changes. If lubricant usage goes up, it could signal that friction has increased in the system.

A fourth way to enhance pump efficiency is to ensure your pumps and piping are sized properly for your infrastructure. Although we’re bringing this up last, it’s really the first step in any pumping operation. If your pumps and piping don’t match, no amount of lubricant or maintenance will help.

Pipes have physical limits to how much fluid they can move at a particular pressure. If pipes aren’t sized properly, you’ll lose efficiency because your motor will have to work harder. It’s like air conditioning - if your ductwork isn’t sized appropriately for your home, you’ll end up paying more on your energy bill.

In this post, we’ve given you the full rundown when it comes to calculating and improving pump efficiency. You can now calculate, measure, and improve pump efficiency, potentially saving your business thousands of dollars annually on energy costs.

For those just getting started with pump optimization, we offer purpose-built, prepackaged solutions that will have you monitoring pump efficiency in minutes, even in hazardous environments.

This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data.

As the viscosity of oil continues to increase and wellbore conditions continue to become more complicated, the lifespan and pump efficiencies of electric submersible pumps and screw pumps commonly used in oilfields have declined, affecting the normal operation of equipment, and the economic benefits have deteriorated year by year. At present, the most commonly used pumps in the exploitation of heavy oil are submersible electric pumps. However, the efficiencies of electric submersible pumps with semi-open impellers are lower than 30% when transporting liquids with viscosities greater than 50 cp, and pump leakage is significant [1,2]. The labyrinth screw pump (or labyrinth pump) is a non-contact power pump and a new type of screw pump with a small flow, high head, and low specific speed. It is suitable for the transport of high-viscosity, high-gas-content, and particle-containing media.

Many scholars have been committed to studying pump theory based on the labyrinth spiral seal mechanism. The earliest scientist who developed the labyrinth screw pump was a Soviet scientist. The purpose of the research and development at that time was to solve the problem of conveying viscous media containing particles. In the labyrinth spiral seal, Golubiev [3] found that the structure of opening a single or multiple threads on the surface of the ring seal could increase the pressure of the sealing liquid in the thread grooves, thereby achieving the purpose of preventing liquid leakage. Bilgen [4] and Karow [5] used laminar and turbulent flow models to numerically analyze the spiral structure of the labyrinth and obtained the flow characteristics in the spiral cavity of the labyrinth under different conditions. Zhu [6] used the laminar flow model to analyze the flow in the labyrinth spiral and obtained the plane flow solution and the spatial flow solution of the oblique section in the honeycomb body. In addition, some researchers have also conducted theoretical analysis and experimental research on the labyrinth seal structure [7,8,9]. These analysis results all showed that the labyrinth spiral structure can produce a greater pumping pressure at high speeds. In terms of the pumping mechanism, Golubiev [10] believed that the pumping pressure of the labyrinth screw pump was caused by the strong turbulent friction of the fluid between the rotor and the stator acting on the threaded wall. Bilgen and Akgungo [4] regarded the fluid flow in the pump as the superposition of the drag flow of the rotor thread on the fluid and the pressure flow under the pressure difference between the two ends of the pump. In terms of structural design, many researchers used computational fluid dynamics (CFD) to numerically simulate trapezoidal, triangular, and rectangular labyrinth pumps, respectively, and analyzed the influence of the thread design parameters on the pumping capacity [11,12,13]. Ma [14] calculated and compared the performances of labyrinth pumps with different thread shapes and found that the rectangular labyrinth screw pump is more suitable for transporting highly viscous media and for multiphase flows.

In the transportation of viscous media, the performance of the labyrinth screw pump is positively correlated to the viscosity of the media, and thus, it can be used in the petrochemical, pharmaceutical, metallurgical, and electric power industries. However, the efficiencies of the currently known labyrinth pumps are very low, which has limited their development. Some scholars have studied the advantages of labyrinth pumps in conveying air-containing, high-viscosity, and other media, but there have been few studies on the structural optimization of labyrinth screw pumps [15,16].

The optimization of a pump structure often depends on data samples collected through experimental design methods and uses various methods, such as Kriging or artificial neural network models, to construct the approximate functional relationship between the optimization parameters and the optimization objective. OPTIMUS, Tosca, and other platforms are used to estimate the functional relationships between the input parameters and output parameters through optimization models and algorithms, and the optimal control parameter combination can be obtained. However, in the process of hydraulic optimization, the optimization is still carried out with the help of design experience, and the optimization results are often not ideal. In contrast to the above optimization models, the essence of the response surface methodology is to replace the model with data. The response surface approach can estimate the variations of the entire design space based on the sample points obtained by the experimental design and graphically express the functional relationship between the input and output. The response surface provides estimated values for the output parameters, and the output function value can be obtained only through the response surface, without the need to perform operations on the original model. Therefore, using the response surface model to optimize the structure of the pump can reduce the calculation time considerably.

Zhang [17] selected a fluoroplastic two-phase-flow centrifugal pump as the research object, adopted the response surface optimization model, and optimized the structure of the pump with the main geometric parameters of the impeller as the optimization parameters to improve the efficiency of the pump and reduce the wear rate. Gao [18] determined the optimization parameters according to the degree of influence of the structural parameters on the objective function and selected the efficiency, shaft power, and head of the pump as the optimization objectives. A response surface optimization model between the structural parameters and the objective function was constructed, and the interactions between the structural parameters were examined.

The structure of the labyrinth screw pump is extremely complex, and the rotor and stator have different structural parameters. Furthermore, the fluid domain involves the handling of dynamic and static interfaces. As a result, the relationship between the objective function and the optimization parameters is difficult to express explicitly, and some optimization parameters are not continuous (the number of stator and rotor screw threads should be rounded according to actual engineering needs). Therefore, the traditional gradient optimization method is not suitable for this study. In response to these problems, we used response surface optimization technology to optimize the structure of the labyrinth pump. Selecting the fluid area of the main part of the rectangular labyrinth screw pump as the research object, the goal was to improve the efficiency and head of the pump and find the best combination of structural parameters.

Section 2 introduces the geometry and operation parameters of the labyrinth screw pump. Section 3 of this article presents the setup and experimental verification of the numerical simulation method. Section 4 describes the process of structural optimization. Section 5 discusses the influence of the internal flow and the oil viscosity on the performance of the labyrinth pump and analyzes the optimization results of the labyrinth pump. This article applies the neural network response surface optimization model to the labyrinth pump, which provides a certain theoretical reference for the design of the labyrinth pump.