mud pump flow rate calculator free sample

Rig pump output, normally in volume per stroke, of mud pumps on the rig is  one of important figures that we really need to know because we will use pump out put figures to calculate many parameters such as bottom up strokes,  wash out depth, tracking drilling fluid, etc. In this post, you will learn how to calculate pump out put for triplex pump and duplex pump in bothOilfield and Metric Unit.

Pump Output per Stroke (PO): The calculator returns the pump output per stroke in barrels (bbl).  However this can be automatically converted to other volume units (e.g. gallons or liters) via the pull-down menu.

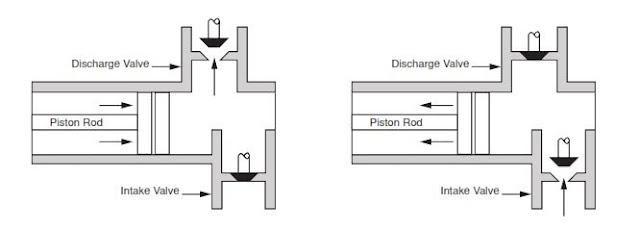
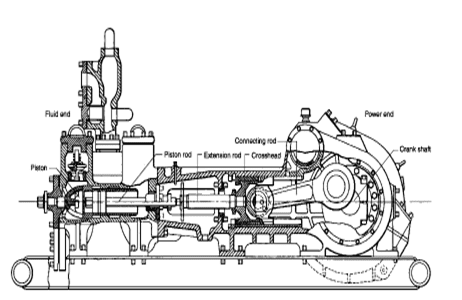
A triplex mud (or slush) pump has three horizontal plungers (cylinders) driven off of one crankshaft. Triplex mud pumps are often used for oil drilling.

Oil and Gas drilling process - Pupm output for Triplex and Duplex pumpsTriplex Pump Formula 1 PO, bbl/stk = 0.000243 x ( in) E.xample: Determine the pump output, bbl/stk, at 100% efficiency for a 7" by 12". triplex pump: PO @ 100%,= 0.000243 x 7 x12 PO @ 100% = 0.142884bbl/stk Adjust the pump output for 95% efficiency: Decimal equivalent = 95 + 100 = 0.95 PO @ 95% = 0.142884bbl/stk x 0.95 PO @ 95% = 0.13574bbl/stk Formula 2 PO, gpm = [3(D x 0.7854)S]0.00411 x SPM where D = liner diameter, in. S = stroke length, in. SPM = strokes per minute Determine the pump output, gpm, for a 7" by 12". triplex pump at 80 strokes per minute: PO, gpm = [3(7 x 0.7854) 1210.00411 x 80 PO, gpm = 1385.4456 x 0.00411 x 80 PO = 455.5 gpm

Example:Duplex Pump Formula 1 0.000324 x (liner diameter, in) x ( stroke lengh, in) = ________ bbl/stk -0.000162 x (rod diameter, in) x ( stroke lengh, in) = ________ bbl/stk Pump out put @ 100% eff = ________bbl/stk Example: Determine the output, bbl/stk, of a 5 1/2" by 14" duplex pump at 100% efficiency. Rod diameter = 2.0": 0.000324 x 5.5 x 14 = 0.137214bbl/stk -0.000162 x 2.0 x 14 = 0.009072bbl/stk Pump output @ 100% eff. = 0.128142bbl/stk Adjust pump output for 85% efficiency: Decimal equivalent = 85 100 = 0.85 PO@85%)= 0.128142bbl/stk x 0.85 PO@ 85% = 0.10892bbl/stk Formula 2

PO. bbl/stk = 0.000162 x S[2(D) - d] where S = stroke length, in. D = liner diameter, in. d = rod diameter, in. Example: Determine the output, bbl/stk, of a 5 1/2". by 14". duplex pump @ 100% efficiency. Rod diameter = 2.0in.: PO@100%=0.000162 x 14 x [ 2 (5.5) - 2 ] PO @ 100%)= 0.000162 x 14 x 56.5 PO@ 100%)= 0.128142bbl/stk Adjust pump output for 85% efficiency: PO@85%,= 0.128142bb/stkx 0.85 PO@8.5%= 0.10892bbl/stk Metric calculation Pump output, liter/min = pump output. liter/stk x pump speed, spm. S.I. units calculation Pump output, m/min = pump output, liter/stk x pump speed, spm. Mud Pumps Mud pumps drive the mud around the drilling system. Depending on liner size availability they can be set up to provide high pressure and low flow rate, or low pressure and high flow rate. Analysis of the application and running the Drill Bits hydraulics program will indicate which liners to recommend. Finding the specification of the mud pumps allows flow rate to be calculated from pump stroke rate, SPM. Information requiredo Pump manufacturer o Number of pumps o Liner size and gallons per revolution Weight As a drill bit cutting structure wears more weight will be required to achieve the same RoP in a homogenous formation. PDC wear flats, worn inserts and worn milled tooth teeth will make the bit drill less efficiently. Increase weight in increments of 2,000lbs approx. In general, weight should be applied before excessive rotary speed so that the cutting structure maintains a significant depth of cut to stabilise the bit and prevent whirl. If downhole weight measurements are available they can be used in combination with surface measurements to gain a more accurate representation of what is happening in the well bore.

Pumps tend to be one of the biggest energy consumers in industrial operations. Pump motors, specifically, require a lot of energy. For instance, a 2500 HP triplex pump used for frac jobs can consume almost 2000 kW of power, meaning a full day of fracking can cost several thousand dollars in energy costs alone!

So, naturally, operators should want to maximize energy efficiency to get the most for their money. Even a 1% improvement in efficiency can decrease annual pumping costs by tens of thousands of dollars. The payoff is worth the effort. And if you want to remotely control your pumps, you want to keep efficiency in mind.

In this post, we’ll point you in the right direction and discuss all things related to pump efficiency. We’ll conclude with several tips for how you can maintain pumping efficiency and keep your energy costs down as much as possible.

In simple terms, pump efficiency refers to the ratio of power out to power in. It’s the mechanical power input at the pump shaft, measured in horsepower (HP), compared to the hydraulic power of the liquid output, also measured in HP. For instance, if a pump requires 1000 HP to operate and produces 800 HP of hydraulic power, it would have an efficiency of 80%.

Remember: pumps have to be driven by something, i.e., an electric or diesel motor. True pump system efficiency needs to factor in the efficiency of both the motor AND the pump.

Consequently, we need to think about how electrical power (when using electric motors) or heat power (when using combustion engines) converts into liquid power to really understand pump efficiency.

Good pump efficiency depends, of course, on pump type and size. High-quality pumps that are well-maintained can achieve efficiencies of 90% or higher, while smaller pumps tend to be less efficient. In general, if you take good care of your pumps, you should be able to achieve 70-90% pump efficiency.

Now that we have a better understanding of the pump efficiency metric, let’s talk about how to calculate it. The mechanical power of the pump, or the input power, is a property of the pump itself and will be documented during the pump setup. The output power, or hydraulic power, is calculated as the liquid flow rate multiplied by the "total head" of the system.

IMPORTANT: to calculate true head, you also need to factor in the work the pump does to move fluid from the source. For example, if the source water is below the pump, you need to account for the extra work the pump puts in to draw source water upwards.

*Note - this calculation assumes the pump inlet is not pressurized and that friction losses are minimal. If the pump experiences a non-zero suction pressure, or if there is significant friction caused by the distance or material of the pipe, these should be factored in as well.

You"ll notice that the elevation head is minimal compared to the discharge pressure, and has minimal effect on the efficiency of the pump. As the elevation change increases or the discharge pressure decreases, however, elevation change will have a greater impact on total head.

Obviously, that’s a fair amount of math to get at the pump efficiency, considering all of the units conversions that need to be done. To avoid doing these calculations manually, feel free to use our simple pump efficiency calculator.

Our calculations use static variables (pump-rated horsepower and water source elevation) and dynamic variables (discharge flow and pressure). To determine pump efficiency, we need to measure the static variables only once, unless they change.

If you want to measure the true efficiency of your pump, taking energy consumption into account, you could add an electrical meter. Your meter should consist of a current transducer and voltage monitor (if using DC) for electrical motors or a fuel gauge for combustion. This would give you a true understanding of how pump efficiency affects energy consumption, and ultimately your bank account.

Up until this point, we’ve covered the ins and outs of how to determine pump efficiency. We’re now ready for the exciting stuff - how to improve pump efficiency!

One of the easiest ways to improve pump efficiency is to actually monitor pumps for signs of efficiency loss! If you monitor flow rate and discharge (output power) along with motor current or fuel consumption, you’ll notice efficiency losses as soon as they occur. Simply having pump efficiency information on hand empowers you to take action.

Another way to increase efficiency is to keep pumps well-maintained. Efficiency losses mostly come from mechanical defects in pumps, e.g., friction, leakages, and component failures. You can mitigate these issues through regular maintenance that keeps parts in working order and reveals impending failures. Of course, if you are continuously monitoring your pumps for efficiency drops, you’ll know exactly when maintenance is due.

You can also improve pump efficiency by keeping pumps lubricated at all times. Lubrication is the enemy of friction, which is the enemy of efficiency (“the enemy of my enemy is my friend…”).

A fourth way to enhance pump efficiency is to ensure your pumps and piping are sized properly for your infrastructure. Although we’re bringing this up last, it’s really the first step in any pumping operation. If your pumps and piping don’t match, no amount of lubricant or maintenance will help.

In this post, we’ve given you the full rundown when it comes to calculating and improving pump efficiency. You can now calculate, measure, and improve pump efficiency, potentially saving your business thousands of dollars annually on energy costs.

For those just getting started with pump optimization, we offer purpose-built, prepackaged solutions that will have you monitoring pump efficiency in minutes, even in hazardous environments.

Pumps are an integral part of almost all industries today. From construction and mining to automotive and aerospace, pumps play a vital role in keeping these industries moving forward. While there are many essential parameters in pumps, one critical parameter is the pump flow rate which becomes a guiding factor for pump manufacturers.

The pump flow rate is one of the most important factors to consider when selecting a pump. It measures how much water the pump can move in a given period of time and is typically expressed in cubic meters/hour (m3/ h). If you’re looking for a pump to use in your home or business, it’s essential to know the flow rate needed to meet your needs. Otherwise, you may end up with a pump that isn’t powerful enough or one that uses more energy than necessary.

The first step is to determine what your needs are. For example, if you’re using the pump to provide water for irrigation, you’ll need to know the maximum flow rate that will be required. Once you know your needs, you can start looking for pumps that have the required flow rate, as you will now be able to give more precise directions to the pump manufacturers about your requirement.

To choose the right pump, it’s also important to consider other factors, such as pump size and efficiency. For instance, a large pump with a high flow rate may be more expensive to purchase and operate than a smaller pump with a lower flow rate. However, it may still be the better option if your water usage is consistently high or you have multiple zones in your irrigation system that need water simultaneously.

Overall, choosing the right pump for your home or business requires careful consideration of all aspects of pumping performance. With the right pump from reliable pump manufacturers, you can rest assured that you’ll always have an adequate supply of water on demand.

Pump flow rate simply refers to the volume of fluid that is moving through a pump in a given time period. There are various units through which it is measured, and they include cubic meter/hour (m3/h), litre/sec (l/s) or gallons per minute (GPM). Different pump manufacturers refer to different pump flow units.

The flow rate of a pump can be affected by several factors, including the size and type of pump, the speed at which it is operating, and the resistance of the system it is pumping into.

Pump Speed: This is the number of times the pump can complete an entire cycle in a minute and is measured in rotations per minute (rpm). The faster the pump speed, the higher the flow rate.

Pump Size: Larger pumps can move more liquid than smaller pumps. This is why it’s essential to choose an appropriately sized pump for your application.

Liquid Density: Heavier liquids (such as oil) will flow more slowly than lighter liquids (such as water). This is because it takes more energy to move a heavier liquid.

Liquid Viscosity: Viscous liquids (such as honey) will flow more slowly than non-viscous liquids (such as water). This is because it takes more energy to move a viscous liquid.

Pipe Size: The larger the pipe diameter, the higher the flow rate. This is because there is less resistance to flow when there is a larger diameter pipe.

Pipe Length: The shorter the length of the pipe, the higher the flow rate. This is because there is less resistance to flow when there is a shorter length of pipe.

Pipe Bends: The fewer the number of bends in the pipe, the higher the flow rate. This is because there is less resistance to flow when there are fewer bends in the pipe.

Now that you know the basics of pump flow rate, you can begin to select a pump that is appropriate for your application. Keep in mind that the factors listed above will all affect pump flow rate, so it’s essential to consider each one when you give your requirements to the pump manufacturers.

Pump speed is measured in revolutions per minute (rpm). To convert from rpm to hertz, divide by 60. For example, if a pump operates at 1000 rpm, its frequency would be 16.67 Hz.

Let’s say you have a pump that is operating at 1000 rpm, has an impeller size of 6 inches, and is pumping water with a density of 62.4 lb/ft3. So the flow rate would be:

The good news is that there are many online flow rate calculators available for free, which you can consider using if you do want to get into too much mathematics.

There are a few key ways to increase the flow rate efficiency in pumps. One is to choose the right pump for the application. Another way is to ensure that the pump is sized correctly for the application. Additionally, regular maintenance can help keep a pump operating at peak efficiency.

When choosing a pump, it is vital to consider the application’s specific needs. For example, if a pump is handling a corrosive fluid, you should select stainless steel or other corrosion-resistant models. Similarly, if the fluid being pumped will be unusually viscous, then a positive displacement pump may be the best option.

Ensuring that a pump is appropriately sized for its application is also critical to maximizing flow rate efficiency. If a pump is too small for the task at hand, it will have to work much harder and will be less efficient. On the other hand, if a pump is too large for the application, it will not operate at peak efficiency.

Finally, regular maintenance is essential to keeping a pump operating at its best. This includes things like inspecting and cleaning the pump regularly and making sure that all of the moving parts are adequately lubricated. By taking these steps, it is possible to keep a pump running at peak efficiency for many years.

In this article provided pump related formulas like fluid flow rate and velocity, power calculation, Specific Speed of Pump (Nq), Total Head, Pump Torque and temperature rise, Net Positive Suction Head, Affinity laws for pump, Pump Efficiency & Overall Efficiency of the Pump

Specific Speed of pump (Nq) is identifies the geometrical similarity of pumps. It is useful to comparing different pump designs irrespective of pump size

Pressure head calculated as per pumping system source tank is under some gauge pressure or vacuum open or open toatmosphericthan pressure head is calculated in metres of water column (MWC) of Feet of water column of liquid.

The amount of NPSH the pump requires to avoid cavitation is called Net Positive Suction Head Required (NPSHr). This value of the pump is determined based on actual pump test by the vendor.

API rated burst strength is de-rated for temperatures from 10 to 600 F° (-12 to 316 C°) Drilling Condition – Gas/oil kick while drilling below the shoe with partial or total mud evacuation (user selects evac percent), with shut in pressurized column of gas/oil to surface and old mud weight gradient behind casing. The old MW that was behind the casing when it was cemented is used for annulus hydrostatic burst calculations and the present MW is used for internal hydrostatic calculations. The user inputs the gas/oil gradient that most closely fits their design for internal pressure gradient.

Production burst loads are calculated assuming a full shut in column of pressured gas/oil (i.e. 100% mud evacuation), with Leakoff EMW pressure at the shoe and a column of salt water behind the casing. .

Drilling collapse loads are calculated assuming the casing has been partially or fully evacuated of mud (resulting from lost circulation, or a blowout), while drilling below the shoe, with a non-pressured column of gas/oil to the surface (i.e. atmospheric pressure at the surface) and a full column of old MW behind the casing. The user inputs the gas/oil gradient that most closely fits their design for internal pressure gradient.

. Production collapse loads are calculated assuming 100% mud evacuation with an un-pressured column of gas/oil to the surface. The old MW that was behind the casing when it was cemented is used for annulus hydrostatic collapse calculations. The user inputs the gas/oil gradient that most closely fits their design for internal pressure gradient.

Cementing Collapse loads are calculated with applicable hydrostatic columns of mud and cement slurries outside the casing and displacement fluid column inside the casing. The small hydrostatic difference of the cement in the shoe joints is ignored and displacement fluid is assumed to the shoe TVD. Cementing collapse is typically a concern with big OD conductors and surface casings.

Tensile Design API rated tensile strengths (body and joint), are de-rated for temps 10 to 600 F (-12 to 316 C). . Drilling and Production Casings are calculated with the same assumptions.

Tensile analysis considers the total hanging weight of the casing as it is being run in the hole. The user selects Vertical or Directional tensile analysis to calculate tensile loads assuming buoyant weight of steel in a mud filled hole. . Buoyancy factor = (65.4-MW)/65.4

Our mission is to provide the world with free and easy-to-use calculators to solve your daily problems. Gone are the days of looking up formulas and blasting away on your physical calculator with a notepad to figure out your problem. Now, software built into websites and apps can do that for you. This can be anything from calculating your monthly payment on a mortgage or figuring out how many calories you can eat to lose weight.