mud pump gear ratio calculator supplier

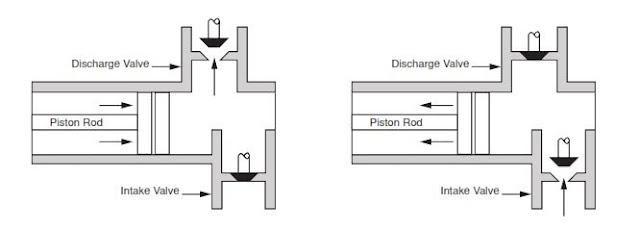
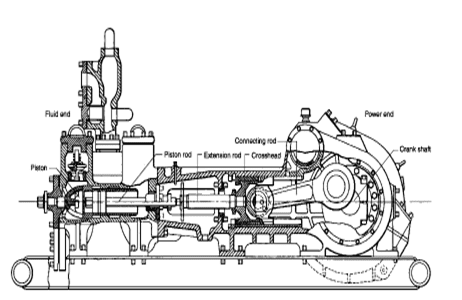
Rig pump output, normally in volume per stroke, of mud pumps on the rig is  one of important figures that we really need to know because we will use pump out put figures to calculate many parameters such as bottom up strokes,  wash out depth, tracking drilling fluid, etc. In this post, you will learn how to calculate pump out put for triplex pump and duplex pump in bothOilfield and Metric Unit.

We provide hydraulic components & repair services for industrial applications like paper mills, saw mills, steel mills, recycling plants, oil & gas applications and mobile applications, including construction, utility, mining, agricultural and marine equipment. This includes hydraulic pumps, motors, valves, servo/prop valves, PTOs, cylinders & parts.

The pump horsepower calculator is used to estimate the pump power, i.e., the power transmitted to the shaft. A pump is one of the most common hydraulic machinery and is used to move fluid by the means of mechanical action by its impeller. Some of its application includes maintaining water supply across the city, heating, ventilation, and cooling systems (HVAC), hydraulics and pneumatics, and electricity generation (see hydroelectric power calculator)

The pump power is a function of hydraulic power and efficiency. Given the importance of this component, it is imperative to understand the basic characteristics of a pump to ensure greater efficiency of the larger processes. You can find more information about pump efficiency and pump power calculations in subsequent paragraphs.

The pump shaft power is defined as the power applied to achieve the head and the volumetric flow rate. It is a function of volumetric flow rate Q, differential head H, the density of fluid ρ, efficiency η, and the gravitational constant g. Mathematically, that"s:

We know that the pumps in most cases do not operate at an efficiency of 100%. Actually, cavitation drastically reduces it. The parameter of specific speed is used to compare the performance of the pump to the ideal case, i.e., a geometrically similar pump delivering 1 cubic meter of fluid per second against 1 m head. The specific speed NsN_\mathrm{s}Ns​ is a dimensionless quantity that is given by the equation:

Note that, while NsN_\mathrm{s}Ns​ is dimensionless, its value changes depending on the units system used for its inputs. The above version of the equation is used in the calculator that gives dimensionless output for specific speed. However, a simpler version of the equation was introduced without the acceleration due to gravity g to use with English units. Mathematically,

The pump horsepower calculator is used to estimate the pump power, i.e., the power transmitted to the shaft. A pump is one of the most common hydraulic machinery and is used to move fluid by the means of mechanical action by its impeller. Some of its application includes maintaining water supply across the city, heating, ventilation, and cooling systems (HVAC), hydraulics and pneumatics, and electricity generation (see hydroelectric power calculator)

The pump power is a function of hydraulic power and efficiency. Given the importance of this component, it is imperative to understand the basic characteristics of a pump to ensure greater efficiency of the larger processes. You can find more information about pump efficiency and pump power calculations in subsequent paragraphs.

The pump shaft power is defined as the power applied to achieve the head and the volumetric flow rate. It is a function of volumetric flow rate Q, differential head H, the density of fluid ρ, efficiency η, and the gravitational constant g. Mathematically, that"s:

We know that the pumps in most cases do not operate at an efficiency of 100%. Actually, cavitation drastically reduces it. The parameter of specific speed is used to compare the performance of the pump to the ideal case, i.e., a geometrically similar pump delivering 1 cubic meter of fluid per second against 1 m head. The specific speed NsN_\mathrm{s}Ns​ is a dimensionless quantity that is given by the equation:

Note that, while NsN_\mathrm{s}Ns​ is dimensionless, its value changes depending on the units system used for its inputs. The above version of the equation is used in the calculator that gives dimensionless output for specific speed. However, a simpler version of the equation was introduced without the acceleration due to gravity g to use with English units. Mathematically,

In our important role as hydraulic pump manufacturers, we are aware of the large number of variables that need to be considered when choosing the right pump for the specific application. The purpose of this first article is to begin to shed light on the large number of technical indicators within the hydraulic pump universe, starting with the parameter “pump head”.

The head of a pump is a physical quantity that expresses the pump’s ability to lift a given volume of fluid, usually expressed in meters of water column, to a higher level from the point where the pump is positioned. In a nutshell, we can also define head as the maximum lifting height that the pump is able to transmit to the pumped fluid. The clearest example is that of a vertical pipe rising directly from the delivery outlet. Fluid will be pumped down the pipe 5 meters from the discharge outlet by a pump with a head of 5 meters. The head of a pump is inversely correlated with the flow rate. The higher the flow rate of the pump, the lower the head.

What is the head of a pump? As mentioned earlier, the head corresponds to the actual energy that the pump delivers to the fluid. The Bernoulli equation is applied between the pump’s inlet and outlet sections:

However, during the design stage, P1 and P2 are never known (as there is no physical element yet and therefore it is not possible to effectively measure the pump’s inlet and outlet pressure).

At this point we can easily calculate the head losses of the system, and therefore choose the correct size of the pump to achieve the desired flow rate at the resulting equivalent head.

The pump head indicator is present and can be found in the data sheets of all our main products. To obtain more information on the technical data of our pumps, please contact the technical and sales team.

In this article provided pump related formulas like fluid flow rate and velocity, power calculation, Specific Speed of Pump (Nq), Total Head, Pump Torque and temperature rise, Net Positive Suction Head, Affinity laws for pump, Pump Efficiency & Overall Efficiency of the Pump

Specific Speed of pump (Nq) is identifies the geometrical similarity of pumps. It is useful to comparing different pump designs irrespective of pump size

Pressure head calculated as per pumping system source tank is under some gauge pressure or vacuum open or open toatmosphericthan pressure head is calculated in metres of water column (MWC) of Feet of water column of liquid.

The amount of NPSH the pump requires to avoid cavitation is called Net Positive Suction Head Required (NPSHr). This value of the pump is determined based on actual pump test by the vendor.

SEEPEX metering and dosing pumps are a range of precision pumps that have a metering accuracy of +/- 1%. The pumps are found in a variety of industrial and municipal applications and are especially suited for low pulsation delivery of low to viscous media as well as chemically aggressive media and media containing solids.